

| Meetkunde probleem (46) |  |
Probleem
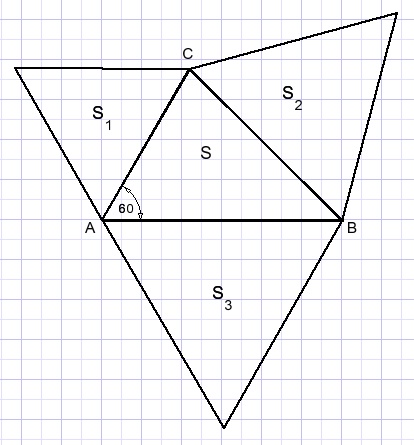
Zie onderstaande figuur.Op de zijden van ΔABC staan gelijkzijdige driehoeken.
LA = 60 graden.
Bewijs dat oppervlakte S + S2 = S1 + S3.
Eerst een aanloopje.
De oppervlakte van een driehoek is basis * hoogte/2.
Een gelijkzijdige driehoek met zijde Z heeft als oppervlakte
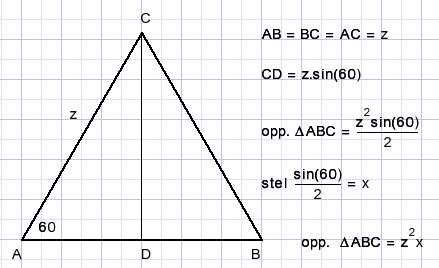
Stel nu in de bovenste figuur dat
- AB=c
- AC=b
- BC=a
Pas de cosinus regel toe in ΔABC:
-
a2 = b2 + c2 - 2bc.cos(60)
cos(60) = 0,5....
a2 = b2 + c2 - bc
vermenigvuldig met x:
a2x = b2x + c2x - bcx
a2x = S2
b2x = S1
c2x = S3
bcx = S....
S2 = S1 + S3 - S
S + S2 = S1 + S3

