

| Meetkunde probleem (45) |  |
Probleem
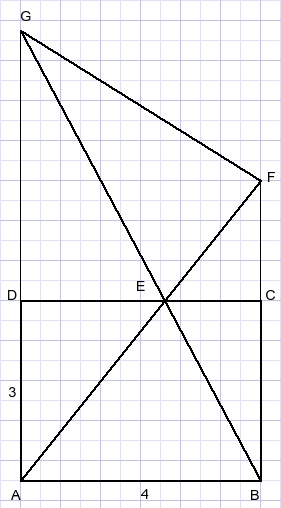
ABCD een rechthoek, AB=4 en AD=3.
Punt E ligt willekeurig op lijn CD.
Bereken de oppervlakte van driehoek EFG.
Dit probleem is om twee redenen interessant:
1. de oppervlakte van driehoek EFG is blijkbaar onafhankelijk van de ligging van E.
2. ik geef 2 oplossingen, de eerste met wat algebra, de tweede zonder.
Notatie: de oppervlakte van bv driehoek ABC schrijf ik als [ABC]
Oplossing (1)
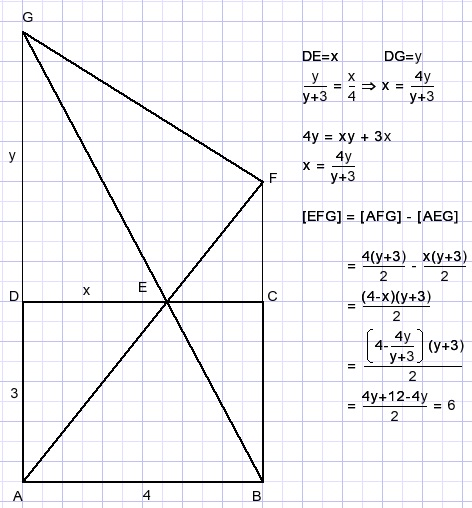
Oplossing (2)
[AFG] = [ABG]..........want gelijke basis en hoogte.
[ABE] = [ABG] - [AEG]
[EFG] = [AFG] - [AEG]
[EFG] = [ABE] = 3*4/2 = 6

