

| Meetkunde probleem (42) |  |
Probleem
Bereken hoek x in onderstaande figuur.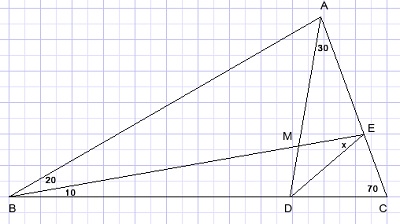
Oplossing (1)
Deze oplossing is van mijzelf.LBAC=50+30=80.
LBEA=10+70=80.
dus:
BA=BE
Trek middelloodlijn van AE.
Verleng DE, F is snijpunt met middelloodlijn.
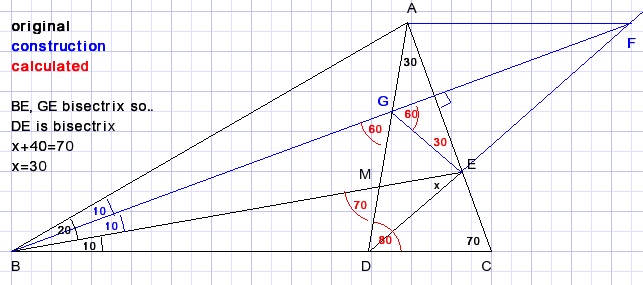
BF snijdt AD in G.
Trek GE.
LFGE=60.
LBDG=60.
dus
LDGE=60.
GE is deellijn van buitenhoek van ΔBDG.
BE is deellijn van LFBC.
Deellijnen gaan door één punt.
DE is dus ook deellijn van LADC=80.
x = 70-40 = 30 graden.
Oplossing (2)
Deze oplossing is van Nelson Tunala en werd gevonden in Facebook groep "classical mathematics".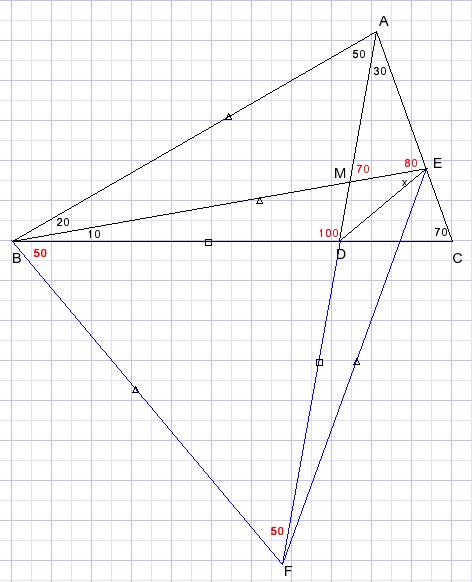
BA=BE (zie oplossing 1)
Verleng AD, punt F ligt zo, dat BF=BA.
LBAF=LBFA=50
BE=BF, LEBF=60 dus ΔBEF is gelijkzijdig.
LDBF=LDFB=50 dus BD=DF.
zodat:
ΔBED congruent is met ΔFED
LBED=LFED.
x = 60 / 2 = 30 graden.
Opmerking
De figuur telt een aantal gelijkvormige driehoeken.Ik heb vergeefs getracht uit de verhoudingen van hun zijden af te leiden dat DA : DC = EA: EC
om te bewijzen dat DE deellijn is.

