meetkunde probleem (37)

Meetkunde probleem (37)

Bereken hoek X in onderstaande figuur:

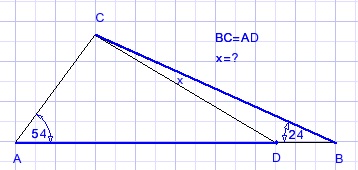
Oplossing

Verschuif BC evenwijdig, zodat punt B op punt D ligt.
(Plaatje wat vergroot voor de duidelijkheid)

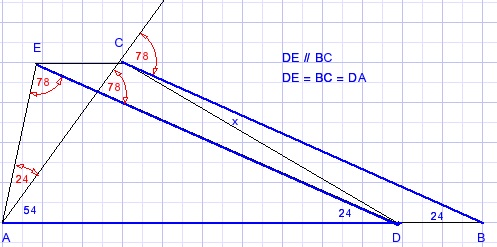
E is het verschoven punt C.
De in rood aanggeven hoeken zijn eenvoudig berekend met het gegeven dat
&delta:ADE gelijkbenig is.
Schuif nu &ADE horizontaal naar rechts tot D op B ligt en E op C.
G is het verschoven punt A.

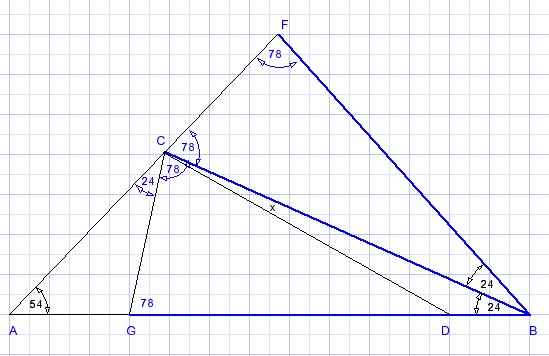
Voeg lijnstuk BF toe met LCBF=24^o.

AF is een rechte lijn.
LAFB=78^o, dus BF = BC.

Punten G,C,F zijn hoekpunten van een regelmatige 15 hoek waarvan B het middelpunt is.
Eerst een tussenstapje, zie plaatje hieronder:

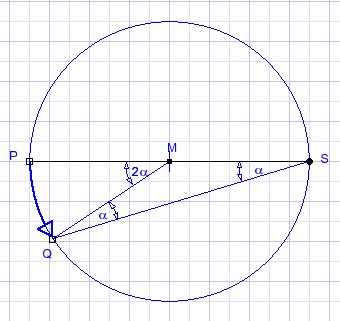
MP draait over hoek 2α naar MQ.
Daardoor draait SP om punt S met een hoek α

Nu de laatste stap (plaatje wat verkleind).
H is midden van CF.
HK is middellijn van de cirkel.

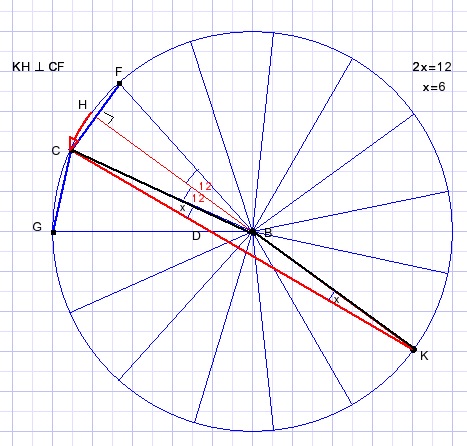
HB draait over een hoek van 12^o naar CB.
KH draait dan 6^o om punt K naar KC.
x = 6^o

naschrift
Voor mijn gevoel moet er een elegantere oplossing zijn.
Wie helpt?