

| Meetkunde puzzel (35) |  |
Opgave
Gegeven is vierhoek ABCD met aangegeven hoeken.
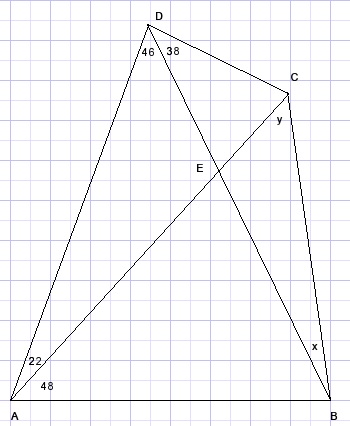
Bereken de hoeken x en y.
Oplossing
Dit soort opgaven is altijd lastig.Mij is geen standaard meetkundige aanpak bekend.
Er komt dus wat intu´tie bij kijken, maar ook gewoon proberen.
Als eerste construeren we de omgeschreven cirkel van driehoek BCE.
Ook verlengen we DC en AB, snijpunt is G.
H is snijpunt van DG met de cirkel.
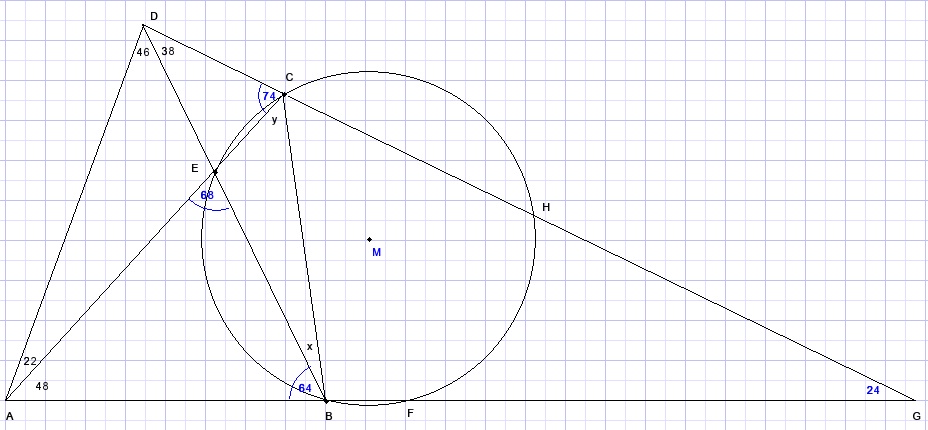
ΔABD....LABD = 64.
ΔACD....LACD = 74.
ΔABE....LAEB = 68
x + y = 68....{buitenhoek ΔBCE}
boogBC = 2x+2y = 136
ΔAGD....LG = 24.
(boogBC - boogFH)/2 = 24
boogFH = 88.
Construeer nu de middelloodlijn van BC.
Deze snijdt de cirkel in punt H' en het verlengde van AG in P.
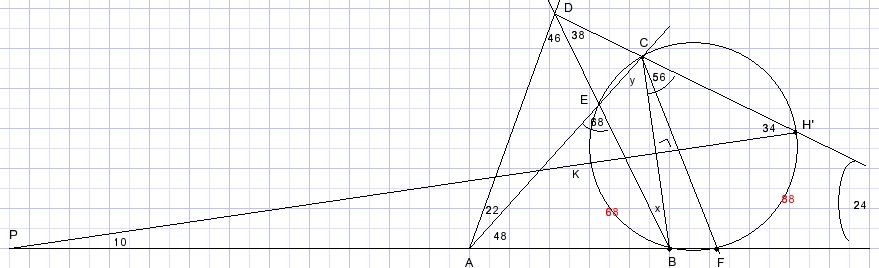
LP = 34 - 24 = 10.
10 = (boogFH'- boogBK)/2.
20 = boogFH' - 68.
boogFH = boogFH' = 88.
De punten H en H' vallen samen.
y = 180 - LACD - 56.
y = 50.
x = 18.

