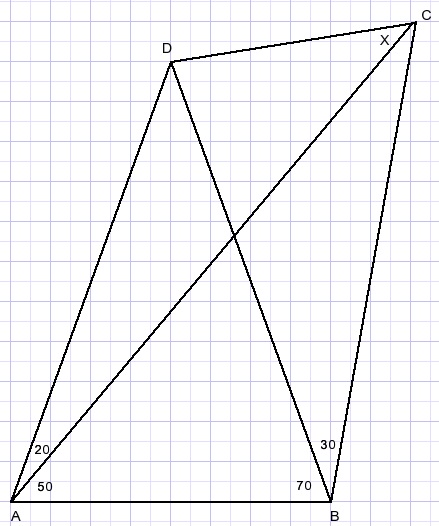
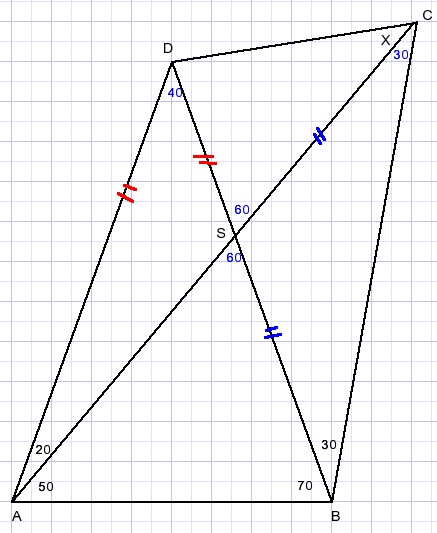
Meetkunde puzzel (29) Opgave: bereken hoek x in onderstaande figuur. Dat is nog niet zo simpel, eerst eens wat hoeken berekenen: We zien twee gelijkbenige driehoeken: ΔABD en ΔBCS. Nu wat intuïtief te werk gaan. Bij gelijkbenige driehoeken gaat de middelloodlijn van de basis door de top. Het snijpunt van de middelloodlijnen van twee zijden van een driehoek is het middelpunt van de omgeschreven cirkel. 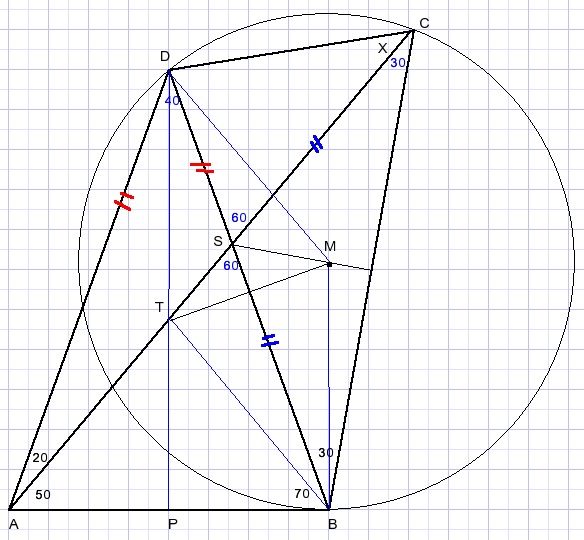We construeren de omgeschreven cirkel van ΔBCD SM is de middelloodlijn van BC. TM is de middelloodlijn van BD. DP is de middelloodlijn van AB. Vierhoek TBMD is een ruit want MB = MD BT = DT diagonalen BD en MT staan loodrecht op elkaar DT en MB zijn dus evenwijdig zodat LABM = 90. AB is raaklijn aan de cirkel. LABD = LBCD want staan op dezelfde cirkelboog. x = LACD = 70 - 30 = 40.