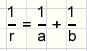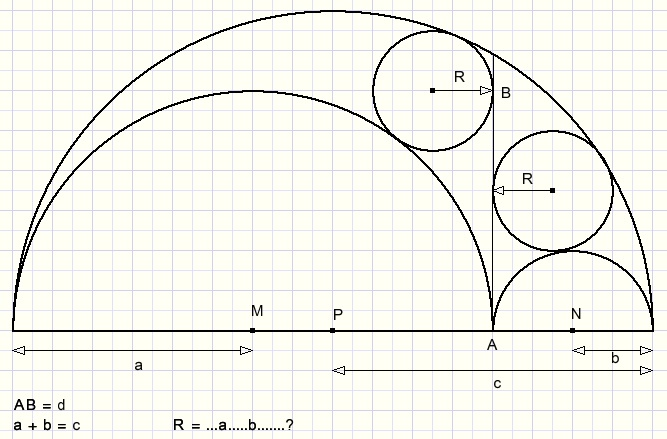
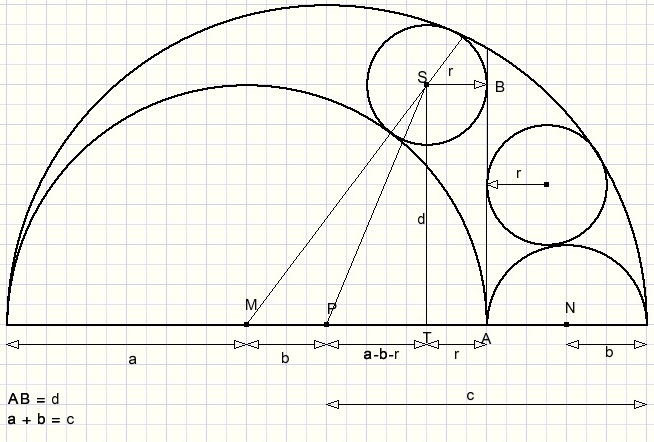
Meetkunde probleem (27) Gegeven zijn: Een halve cirkel met middelpunt P en straal c en daarbinnen twee andere halve cirkels met middelpunten M en N en straal a en b. c = a + b. Daarbinnen twee kleine cirkels met straal r, die de andere cirkels raakt evenals de loodlijn AB. Gevraagd: Druk R uit in a en b. Zie het volgende plaatje: We berekenen de afstand d = ST twee maal: - binnen ΔPTS - binnen ΔMTS Dan stellen de deze waarden van d aan elkaar gelijk en vereenvoudigen de vergelijking. r blijkt het harmonisch gemiddelde te zijn van de stralen a en b. Ook is te schrijven