

| meetkunde puzzel (26) |  |
Opgave:
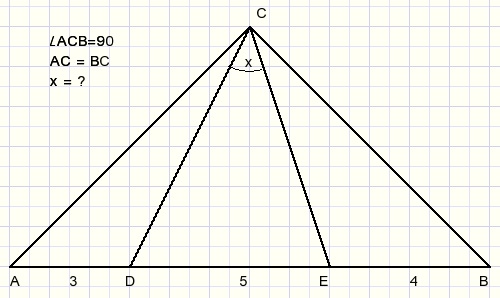
Bovenstaand zien we rechthoekige en gelijkbenige driehoek ABC.
Bewijs in bovenstaande figuur dat x = LDCE = 45 graden.
We zien de afstanden AD=3, DE=5 en EB=4.
Dat is een Pythagoras drietal.
We pakken dit probleem wat algemener aan.
Stel AD=a, DE=c en EB=b en a2 + b2 = c2.
Te bewijzen dat x = 45.
Bewijs
Verschuif lijnstukken AD en EB evenwijdig aan AB totdat ze elkaar raken in punt E.Wegens gelijkvormigheid van ΔABC en ΔDEM (gelijke hoeken) is
MD = ME.
We bewijzen nu dat ook MC = MD = ME.
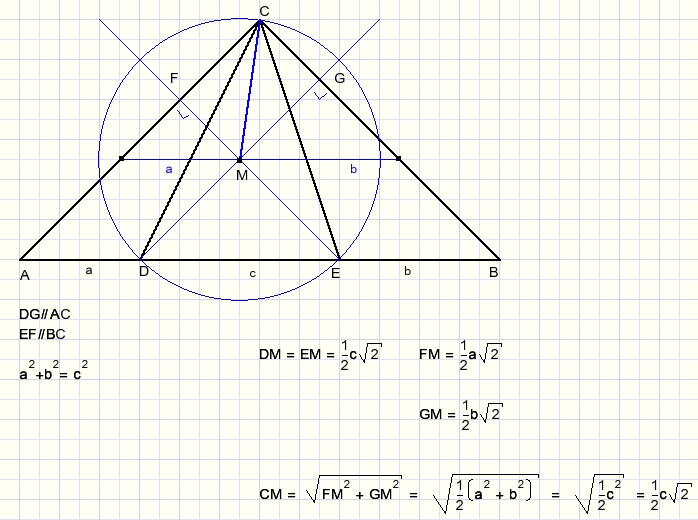
Opmerking: in een gelijkbenige rechthoekige driehoek met schuine zijde a
zijn de rechthoekszijden de helft van de wortel uit de schuine zijde.
M is dus middelpunt van de cirkel door de punten D, E en C.
LDME staat op een cirkelboog DE van 90 graden.
Hoek x staat ook op DE dus LDCE = 45.

