

| Meetkunde probleem (25) |  |
Onderstaand meetkunde probleem trof ik aan in de FaceBook groep "Matematika".
Het was gepubliceerd door Doaa Jayab.
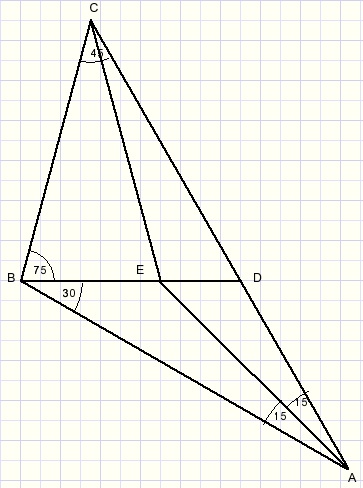
Vraag:
bewijs in bovenstaande figuur dat CE=AE
Oplossing 1
Trek lijn BF, LDBF=30.Bekijk ΔBCF : LCBF=45 , BF=CF
Bekijk ΔBCD : LCDB=60...{180-75-45}
Bekijk ΔABD : LABD=30...{60-30}
Bekijk ΔABF : LAFB=90...{180-60-30}
Trek lijn EG // BF
Trek lijn EF.
We gaan nu bewijzen dat CG=AG zodat wegens congruente driehoeken CEG en AEG geldt dat CE=AE.
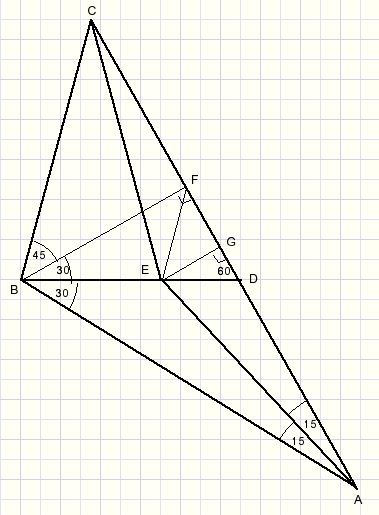
Punt E is het snijpunt van de deellijnen van ΔABF..{deelijnen van een driehoek gaan door 1 punt}
LEFG=45
Voor de duidelijkheid vergroten we een stukje van de figuur:
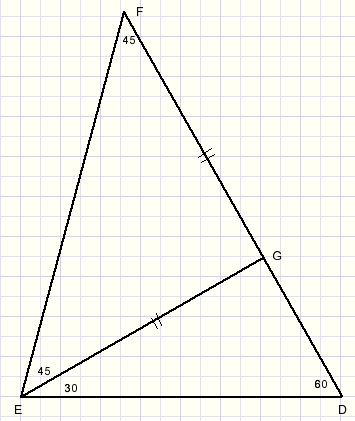
Bekijk ΔEFG...EG=FG...{basishoeken 45 graden}
Bekijk ΔEDG...ED=2*DG...{helft gelijkzijdige driehoek}
Stel DF=1.
Stel DG=x. dan DE=2x

zodat:
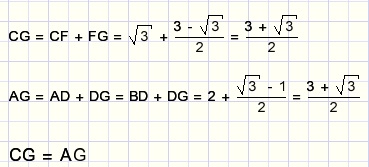
Oplossing 2
We gaan uit van de eerste figuur.Trek lijnen BH en EH zo, dat LABH = 30 en EH loodrecht op AB
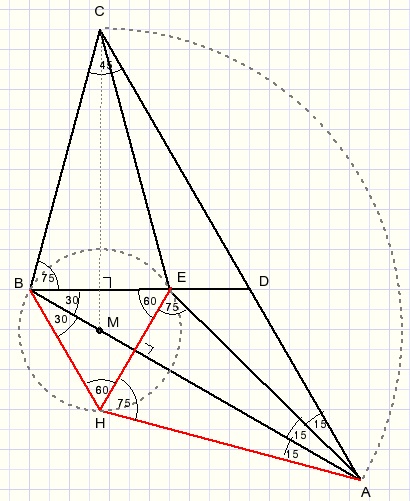
ΔBEH is gelijkzijdig.
ΔAEH is gelijkbenig: AH = AE.
M is middelpunt van de omgeschreven cirkel van ΔBEH.
ΔEHA is congruent met ΔBEC...{ZHH}
AE = BC = CE.

