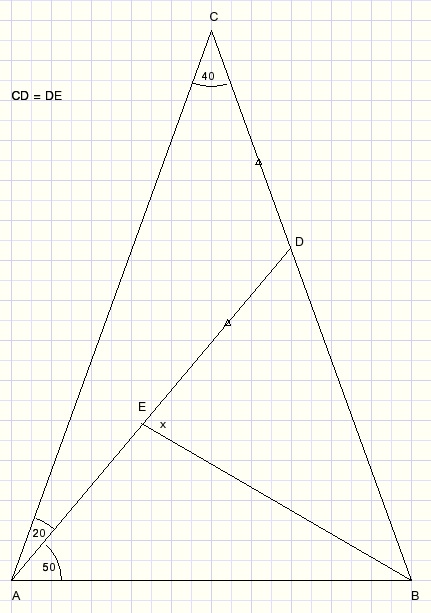
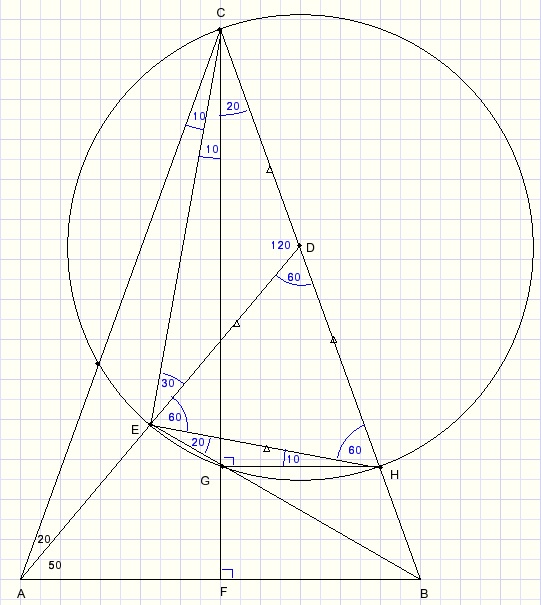
meetkunde probleem (24) Zie onderstaand probleem. Bereken de grootte van hoek x. Driehoek ABC is gelijkbenig, AC = BC, wegens LB = LA = 70. Punt D is middelpunt van de cirkel door C en E. Deze cirkel snijdt BC in punt H. Trek lijnen CE en EH. Teken middelloodlijn van AB. Teken punt G op CF zo, dat HG loodrecht op CF. Bekijk ΔADC. LADC = 180 - 20 - 40 = 120 LADB = 180 - 120 = 60. DE = DH zodat LDEH = LHED = (180 - 60)/2 = 60. G ligt op de cirkel omdat LCGH = 90. LHEG = LBCF = 20 want staan beide op boog GH. x = LDEB = 20 + 60 = 80. Blijft over de vraag of punt G op lijn BE ligt. LAEB = 180 - 60 - 20 = 100. LABE = 180 - 100 - 50 = 30. LFGB = 90 - 30 = 60. LCGE = 120/2 = 60 want staat op boog CE. Punt G ligt dus op lijn BE.