

| meetkunde puzzel (22) |  |
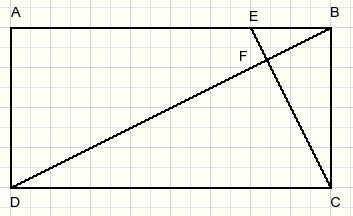
Hieronder staat rechthoek ABCD met BD loodrecht op CE.
Bewijs dat BE x BA = (BC)2.
Dit doet denken aan "de macht van een punt t.o.v. een cirkel".
Dus eerst wat theorie.
De macht van een punt t.o.v. een cirkel
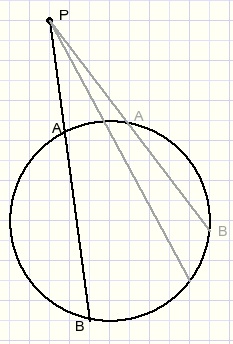
Vanuit een willekeurig punt P buiten een cirkel trekken we een lijndie de cirkel snijdt in de punten A en B.
Nu doet zich een opmerkelijk verschijnsel voor:
het product van de afstanden PA x PB is steeds hetzelfde, welke lijn door P we ook trekken.
Dit produkt heet "de macht van P t.o.v. de cirkel".
bewijs
-
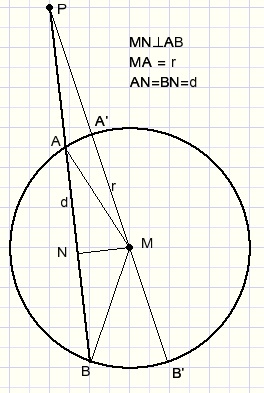
PA.PB = (PN-d)(PN+d) = PN2 - d2.....1)
PN2 = PM2 - MN2.....2)
MN2 = r2 - d2.....3)
..2) + ..3) :
PN2 = PM2 - r2 + d2.....4)
..1) + ..4):
PA.PB = PM2 - r2 + d2 - d2 = PM2 - r2 = (PM-r)(PM+r) = PA' . PB'
Oplossing 1
We beschouwen de cirkel door de punten A, E en C en de macht van B t.o.v. deze cirkel.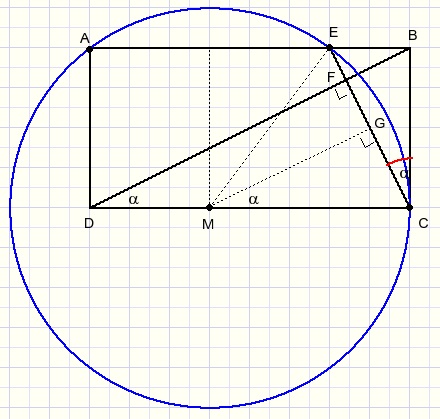
BE.BA = BC2 als BC raaklijn is van de cirkel oftewel:
Het middelpunt van de cirkel op de lijn CD ligt.
M is het snijpunt van de middelloodlijn van AE met CD.
Trek MG loodrecht op CE.
MG is middelloodlijn van CE wegens de congruentie van driehoeken MGE en MGC.
M is het snijpunt van middelloodlijnen dus middelpunt van de cirkel.
Omdat de macht van B t.o.v. de cirkel vast staat geldt: BE.BA = BC2.
Oplossing 2
Dit bewijs maakt gebruik van gelijkvormige driehoeken.Zie de figuur hierboven:


