| meetkunde puzzel (20) |  |
Opgave: bereken de hoek x in onderstaande figuur.
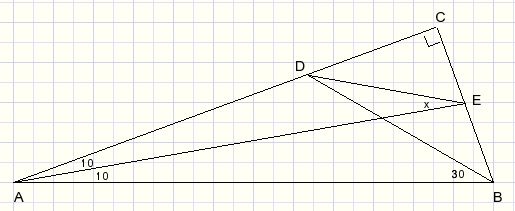
Wederom een vrij lastig probleem.
De rechte hoek C ligt op de cirkel met DE als middellijn.
Maar C ligt ook op de cirkel met AB als middellijn.
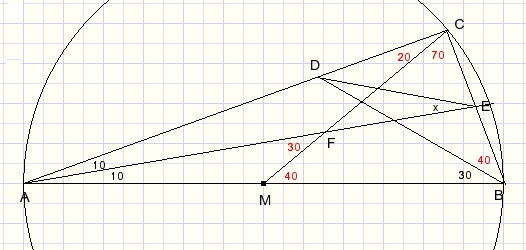
We tekenen de cirkel door A,B en C met middelpunt M.
Ook trekken we lijn CM, die AE snijdt in F.
De met rode cijfers aangegeven hoeken zijn eenvoudig te berekenen.
Teken nu de cirkel door de punten C,D en E.
F ligt ook op de cirkel:
-
boog DF = 2*20 = 40
boog CE = 2*30 = 60
LCAB = (60 - 40)/2 = 10...klopt!
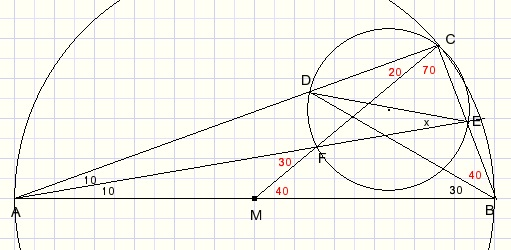
LDCF = 20 graden en staat op boog DF.
Lx staat op dezelfde boog, dus is ook 20 graden.
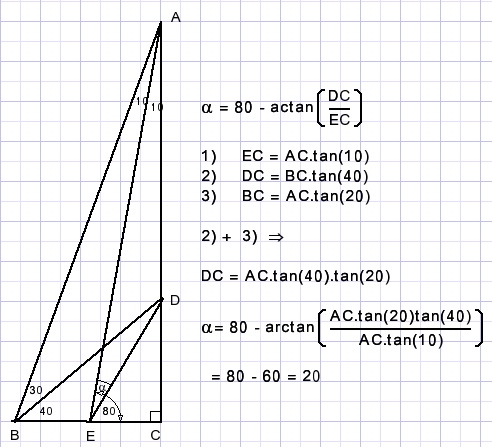
Ernst Granneman wees mij op een slordigheid in het bewijs hiervoor.
Die heb ik gecorrigeerd.
Ook stuurde hij deze mooie goniometrische oplossing mee: