

| meetkunde puzzel (18) |  |
Deze meetkunde puzzel is afkomstig van de Facebook groep "Classical Mathematics".
De oplossingen zijn deels van mijzelf.
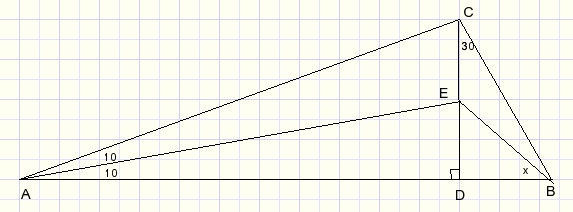
Opgave : bereken hoek x.
Er zijn een paar methoden mogelijk.
1.Gonionetrie + rekenmachine
Dit is de eenvoudigste weg.Stel BD = 1.
Dan is
DE = tan(x)
DC = tan(60)........1)
DE = AD.tan(10).......2)
DC = AD.tan(20).......3)
combinerend:

Rekenmachine:
DE = 0,839099631
x = arctan(0,839099631) = 40
2.Goniometrie zonder rekenmachine
DE = tan(40)Vermenigvuldig in de laatste vergelijking .1) teller en noemer met tan(40)
zodat moet gelden:
tan(60).tan(10) = tan(20).tan(40), want dan blijft na deling tan(40) in de teller over.
Meetkundige interpretatie:
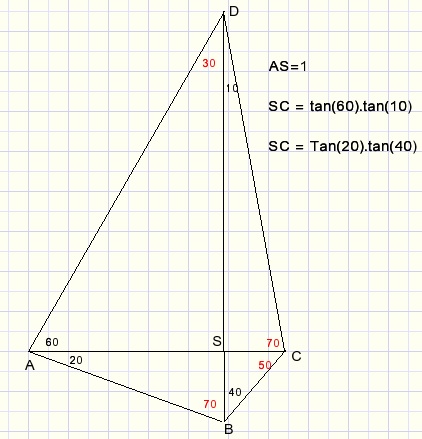
Zie vierhoek ABCD hierboven.
De grootte van de gegeven hoeken is zwart aangegeven.
Driehoeken ASD, ASB, CSD kunnen we construeren.
Maar heeft driehoek BCS dan scherpe hoeken 40 en 50 graden?
Wie helpt?
3.Meetkundige oplossing
We gaan uit van de eerste figuur en verlengen zijden AC, AE om gelijkbenige driehoek ABG te verkrijgen.AF is middelloodlijn van BG.
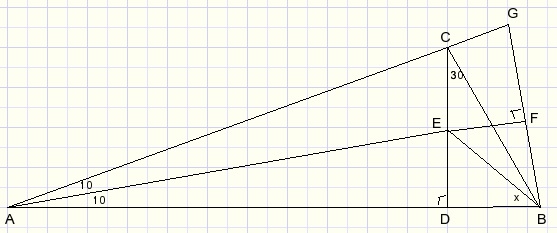
LFEB = x+10..........{buitenhoek van ΔABE}
Voor de duidelijkheid vergroten we nu een stukje:
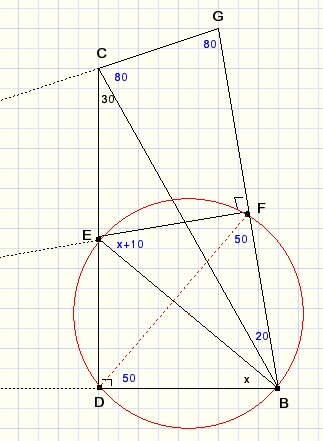
2DB = BG....{wegens LDBG=60}
2BF = BG....{wegens F middelpunt BG}
zodat
BD = BF
LDBF=80
LBDF=LBFD=50
Trek nu de omgeschreven cirkel van vierhoek DBFE....{BE is middellijn wegens rechte hoeken D en F}
LFEB=LFDB....{staan beide op boog BF}
x+10 = 50
x = 40

