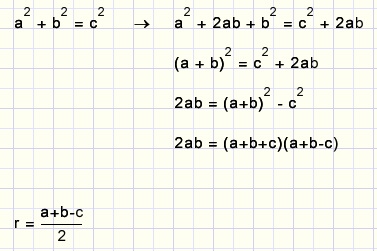| meetkunde puzzel (17) |  |
Onderstaande figuur toont een rechthoek met daarin rechthoekige driehoeken met hun ingeschreven cirkels.
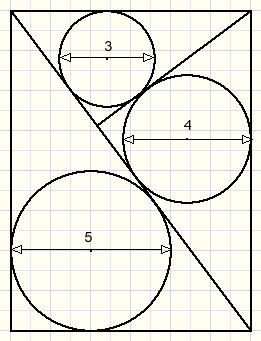
Vraag: bereken de oppervlakte van de rechthoek in bovenstaande figuur.
Bekijk onderstaande figuur:
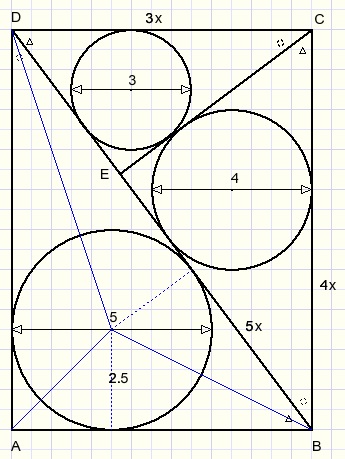
Driehoeken DEC, CEB en BAD zijn gelijkvormig.
Zie gelijke merktekens in gelijke hoeken.
De ene driehoek is een vergroting van de andere.
Overeenkomstige lijnen in de driehoeken hebben daarom dezelfde verhouding.
De shuine zijden van de driehoeken zullen zich dus verhouden als 3:4:5,
dezelfde verhouding als de diameters van de ingeschreven cirkels.
Stel nu:
-
AB=3x
BC=4x
BD=5x
wat ook uit de stelling van Pythagoras volgt.
De oppervlakte van driehoek ABD is (basis x hoogte / 2)
-
0,5 . 2,5 . 3x + 0,5 . 2,5 . 4x + 0,5 . 2,5 . 5x = 15x.
-
0,5 . 4x . 3x = 6x2
-
15x = 6x2
volgt
x = 2,5
-
3 . 2,5 . 4 . 2,5 = 75
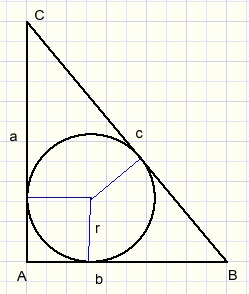
Toevoeging
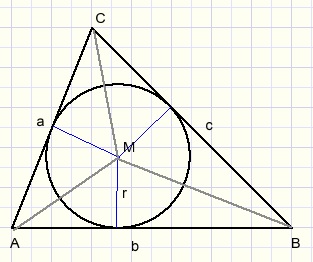
Als we de oppervlakte van een driehoek ABC schrijven als [ABC]
dan geldt voor de straal r van de ingeschreven cirkel (zie figuur hierboven):
-
0,5ra + 0,5rb + 0,5rc = [ABC]
Kan die formule vereenvoudigd worden als LA recht is? Zodat geldt:
-
a2 + b2 = c2
2[ABC] = ab
Daar gaan we: