meetkunde puzzel (16)

Gegeven is driehoek ABC met daarbinnen punt P. Zie figuur:



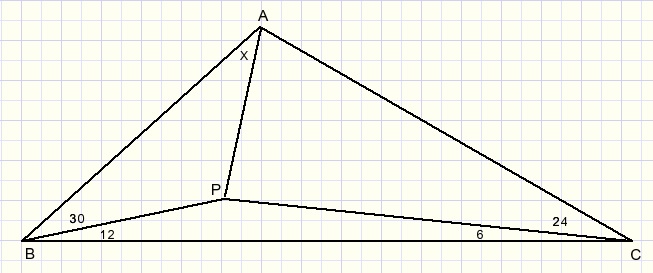
Gevraagd: de hoek x te berekenen.

In principe zijn dit soort problemen aan te pakken met goniometrie: cosinus en sinus regel.
Geef een zijde een willekeurige lengte en bereken de andere zijden waaruit weer de hoekgrootten volgen.

Maar in deze figuur zit regelmaat (veelvouden van 6, som 30 graden) zodat een
puur meetkundige oplossing mogelijk lijkt.

Een simpel probleem is dit niet.
We zien een driehoek met lijnen vanuit de hoekpunten die elkaar snijden in P.
Een oplossing begint met te bedenken of dit lijkt op iets bekends.
De deellijnen van de hoeken van een driehoek gaan door 1 punt.
Maar hier zien we geen deellijnen.
Eens de omgeschreven cirkel tekenen van driehoek ABC.



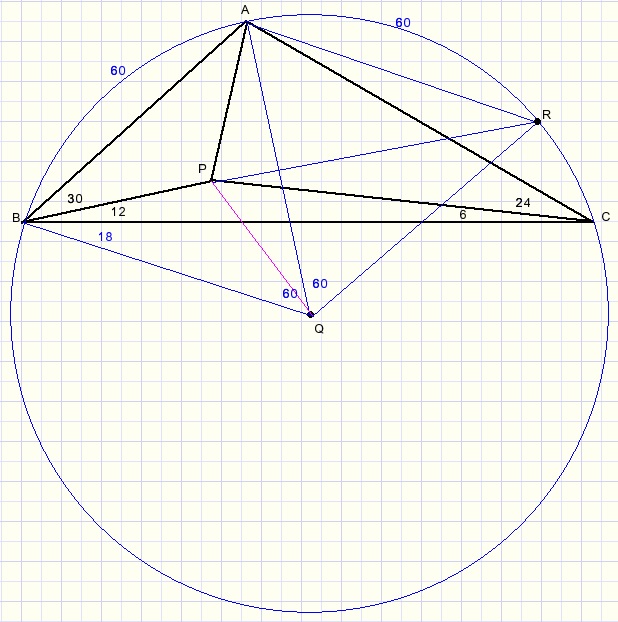
Het middelpunt van die cirkel is Q, teken QB, QA en QR.
R ligt op de verlengde lijn BP.
Toepassing van de stelling van Thales voor hoekpunten B en C levert dan een verrassende kijk op:
(zie appendix 2 voor uitleg)
    - boog AB = boog AR = 60 graden.
    - driehoeken ABQ en AQR zijn gelijkzijdig.
    - vierkant ABQR is een ruit zodat AQ en BR loodrecht op elkaar staan.
    - PA = PQ (wegens symmetrie).
    - LCBQ = 18 graden.
    - BP is deellijn van LB.
Nu tekenen we de omgeschreven cirkel van driehoek APC erbij.
Het plaatje hieronder klopt als LPAV = 90 graden want dan is PV middellijn.



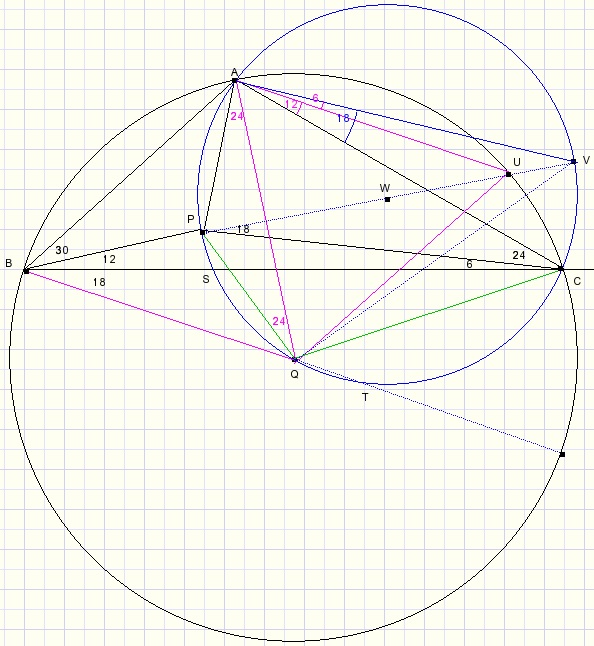
    - LCAU = LPBC = 12 (boog UC = 24)
    - LCAV = LVPC = 18 (boog VC = 36)
    - LVAU = 18 - 12 = 6
    - LPAQ = 24 (boog PQ = 48)
    - LPAV = 24 + 60 + 6 = 90 graden


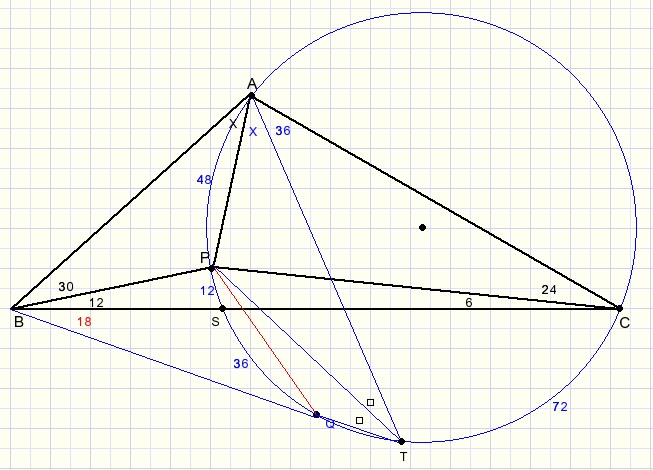
LATP = LPTQ = 24 graden.
PT is bisectrice van LT.

LCBT = 18 = (boog CT - boog QS)/2, zodat boog CT = 72 en LCAT = 36.

De deellijnen van de hoeken van een driehoek gaan door één punt zodat ook AP deellijn is.
LA = 180 - 42 - 30 = 108 graden.
2x + 36 = 108
x = 36.

Appendix 1

Goniometrische berekening van x:

stappen
    1. stel AB=1.
    2. bereken BC met sinusregel.
    3. bereken BP met sinusregel.
    4. bereken AP met cosinusregel.
    5. bereken x met sinusregel



Appendix 2

De stelling van Thales. (Grieks wiskundige 624 - 547 v.Chr.)

Hoeken meten met cirkelbogen:
definitie:
    met de grootte van een cirkelboog bedoelen we de grootte van de middelpuntshoek.


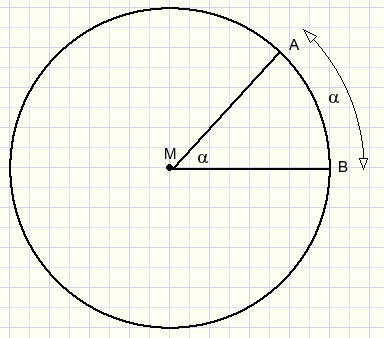
stelling
    een hoek op een cirkelboog is gelijk aan de helft van die boog


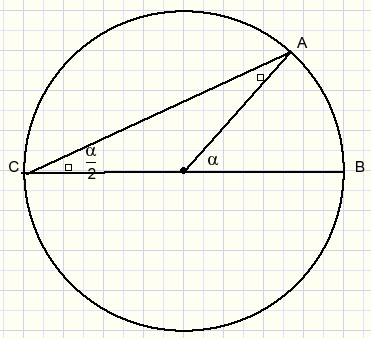
hoek C is de helft van boog AB.
Het bewijs volgt direct uit de gelijkbenige driehoek AMC en de regel dat
een buitenhoek van een driehoek gelijk is aan de som van de niet aanliggende binnenhoeken.
Dat geldt voor elke willekeurige boog, wat te zien is met optellen van bogen.



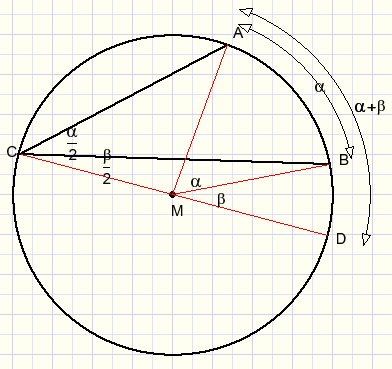
Met de stelling van Thales zijn ook regels af te leiden voor hoeken die buiten of binnen de cirkel liggen.



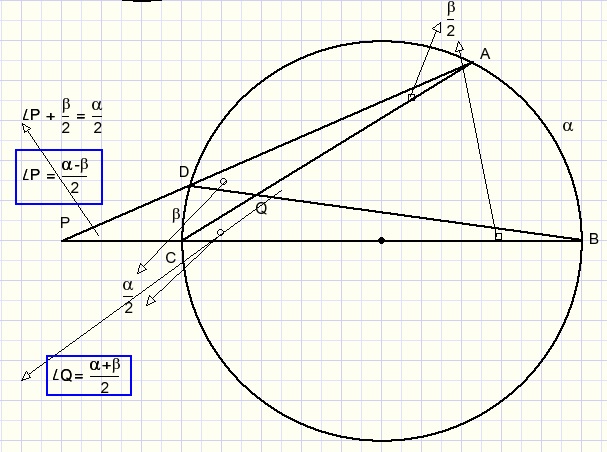
    - een binnenhoek is gelijk aan de helft van de som van de cirkelbogen.
    - een buitenhoek is gelijk aan de helft van het verschil van de cirkelbogen.
Wederom een makkelijk geval waar één been van de hoek door het middelpunt loopt.
Maar door optellen van bogen is te zien dat de regels altijd gelden.