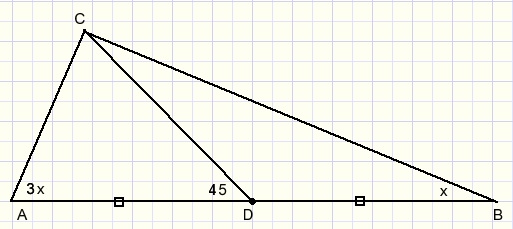
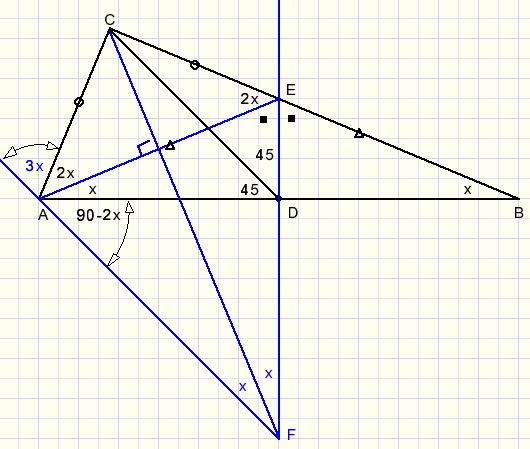
meetkunde probleem (14) Het volgende meetkunde probleem trof ik aan in de Facebook groep "PI love math". AD=DB Vraag: bewijs dat x=22,5 Het bewijs stap 1: trek de middelloodlijn van AB. E is snijpunt met BC. trek AE. LDAE=LDBE=x LAEC=x+x=2x.....(buitenhoek ΔABE) LCAE=2x Conclusie: AC=EC stap 2: trek middelloodlijn van AE, snijpunt met vorige middelloodlijn is F trek FA. LAEF=90-x LEFC=LAFC=x LDAF=90-2x stap 3: beschouw ΔADF FC is deellijn van binnenhoek F. DC is deellijn van buitenhoek D. conclusie: AC is deellijn van buitenhoek A. stap 4: beschouw de hoeken rond punt A. 3x + 3x + 90-2x = 180 4x=90 x=22,50