

| meetkunde probleem (13) |  |
Opgave: bereken de hoek x in onderstaande figuur:
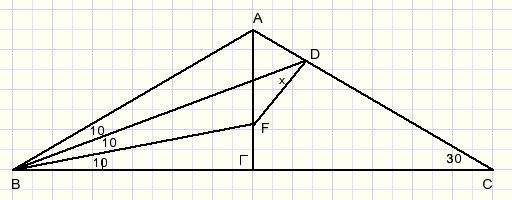
Hiervoor is een hulpstelling vereist:
-
de buitendeellijnen van twee hoeken van een driehoek en de deellijn van de derde hoek gaan door één punt
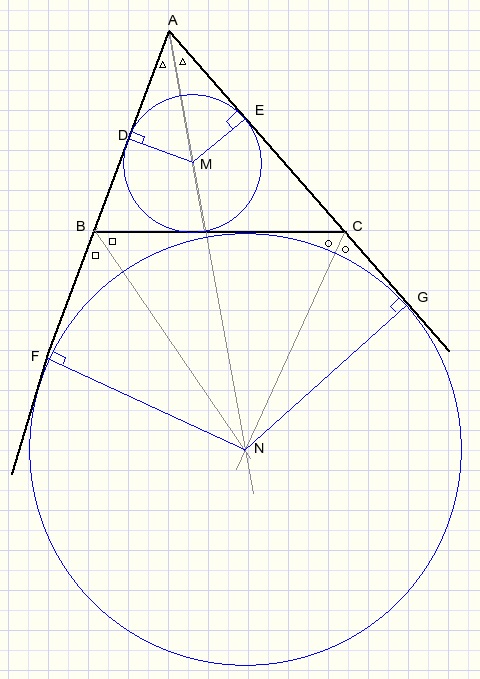
Beschouw de figuur hierboven:
M is het snijpunt van de deellijnen van ΔABC.
N is het snijpunt van de deellijnen van buitenhoeken B en C.
M en N zijn de middelpunten van de in- en aangeschreven cirkel.
Lijnen DM en FN staan beide loodrecht op AB.
LAMD=LANF.
AN is dus een rechte lijn.
De oplossing
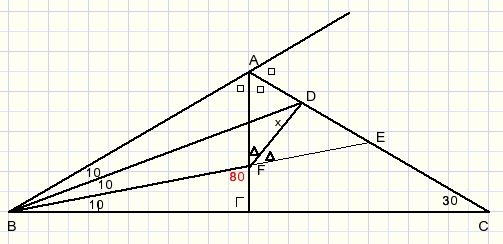
1. trek lijn BA wat door
2. beschouw nu ΔABF
3. BD is deellijn van binnenhoek B
3. AC is deellijn van buitenhoek A
4. D is snijpunt van deellijnen dus DF is de deellijn van buitenhoek F
5. LAFE=800
6. LAFD=0,5*80=400
7. x+10 = 40
8. x = 300

