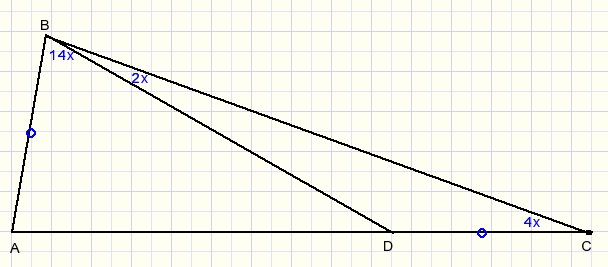
meetkunde probleem (12) Het volgende meetkunde probleem trof ik aan op Facebook. (in groep "Classical Mathematics"). Ook trof ik een plaatje aan met de oplossing, maar de stappen erheen werden niet vermeld. De volgende oplossing is dus niet van mijzelf, maar de stappen heb ik wel gereconstrueerd. Dit is het probleem: Gegeven is 1. ΔABC met op BC het punt D zo dat AB=DC. 2. De grootte van enkele hoeken, zie figuur (in blauw). Gevraagd: bereken de waarde van x. Bij deze berekening maken we enkele keren gebruik van deze stelling: de buitenhoek van een driehoek is gelijk aan de som van de niet aanliggende binnenhoeken. 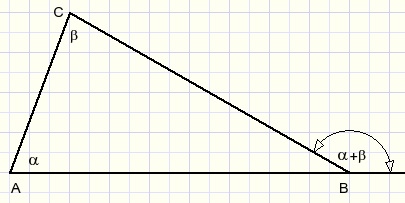Zie dit plaatje: de berekening Stap 1. Cirkel DC om vanuit D. P is het snijpunt met BC, zodat DP=DC en dus ook LDPC=LPCD=4x. 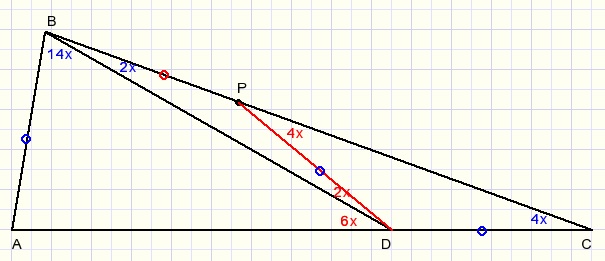LADB=6x want buitenhoek van ΔBCD LADP=8x want buitenhoek van ΔDCP LBDP=8x-6x=2x LPBD=LPDB zodat BP=DP dus ook AB=BP (=PD=DC) Stap 2. Trek de deellijn BE van LABC. Punt E op AC. 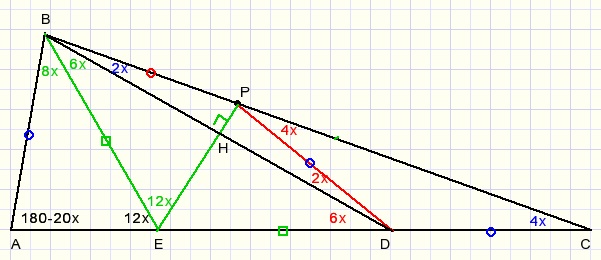LAEB=12x want buitenhoek van ΔBEC LAEB=LPEB=12x wegens congruentie ΔBEA en ΔBEP LEBD=LBDE=6x zodat EB=ED EP is dus middelloodlijn van BD, alle hoeken bij H zijn 900 Stap 3. LBEP=LDEP=12x wegens congruentie ΔPEB en ΔPED Bekijk punt E: 36x=1800 x=5 Een lastig probleem.