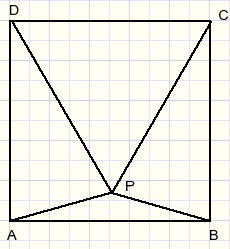
meetkunde probleem (11) Bij mijn puzzels staat het volgende meetkunde probleem (67): Gegeven is vierkant ABCD. Driehoek CDP is gelijkzijdig. Gevraagd is de grootte van LBAP. Die berekening is niet heel moeilijk en de uitkomst is 150. Maar het probleem wordt een stuk lastiger na omdraaiing: Gegeven is vierkant ABCD en een punt P erbinnen zodanig dat LPAB = LPBA = 150. Bewijs nu, dat driehoek CDP gelijkzijdig is. Hoe pak je zo'n bewijs aan? Met alleen de hoek van 150 komen we niet ver. Er moet gebruik gemaakt worden van het feit dat ABCD een vierkant is. Laten we daarom de figuur eens spiegelen om diagonaal AC. 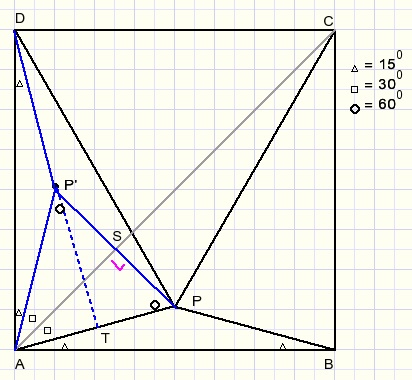Dat levert het volgende plaatje, beetje vergroot voor de duidelijkheid: Punt P' is de spiegeling van P ten opzichte van lijn AC. Bekijk nu eerst driehoek APP'. Daarin is AP = AP' en LPAP' = 90 - 2*15 = 600. LAPP'= (180 - 60)/2 = 600 zodat driehoek APP' gelijkzijdig is. Trek nu lijnstuk DP'door tot T op AP. LATD = 180-15-15-60 = 900 P'T is hoogtelijn in een gelijkzijdige driehoek waardoor punt T het midden is van AP. DT is dus middelloodlijn van AP. Daarom geldt DA = DP, dus ook DP = DC en wegens symmetrie: CP = CD. Driehoek CDP is gelijkzijdig. Mogelijk is er een kortere, betere of creatievere oplossing. Laat het mij weten, dan publiceer ik die hieronder met uiteraard vermelding van uw naam.