meetkunde puzzel

meetkunde puzzel numeriek opgelost

Het probleem

In dit artikel beschrijf ik de numerieke oplossing van een lastig meetkundig probleem.
Later lukte het ook de oplossing meetkundig te vinden, zie [HIER].

Dit is het probleem:

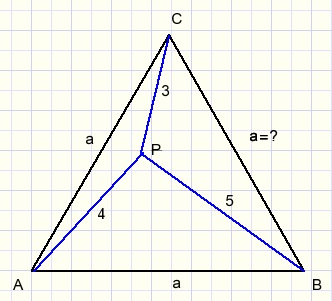
Gegeven is gelijkzijdige driehoek ABC met daarbinnen een punt P zodat:

Gevraagd: de lengte a van de zijden van de driehoek.

De oplossing

We beginnen met een gok voor de grootte van LACP.
Met deze hoek bekend is met de sinusregel LCAP en AC te berekenen.
Dan is ook LPAB bekend en op dezelfde manier is dan AB te berekenen.
Was de gok van LACP correct dan vinden we AC = AB.

Hoe gokken we LACP op nette wijze?
Met drie variabelen die in het programma angle, amin en amax heten.
amin is de minimale waarde van de hoek, amax de maximale.
angle is de gok voor LACP.
Die gok steeds : angle = (amin + amx)/2.

Nu zijn er twee soorten uitkomsten:

In geval 1. reageert het programma met amax = angle
en in geval 2. is dat amin = angle.
De waarde van variabele angle wordt dus ingeklemd tussen amin en amax, het verschil halveert bij elke stap.
De gok herhaalt zich totdat het verschil |AC-AM| < 0,000001 is.

Data

const deg2rad = pi/180;
      rad2deg = 180/pi;

type TG3 = record
            a : double;
            b : double;
            c : double;
            alpha : double;
            beta  : double;
            gamma : double;
           end;

procedure triangle(var G3 : TG3);
//given: a,b,alpha
//calculate : c, beta, gamma
begin
 with G3 do
  begin
   beta := arcsin(b*sin(alpha)/a);
   gamma := pi - alpha - beta;
   c := a*sin(gamma)/sin(alpha);
  end; 
end;

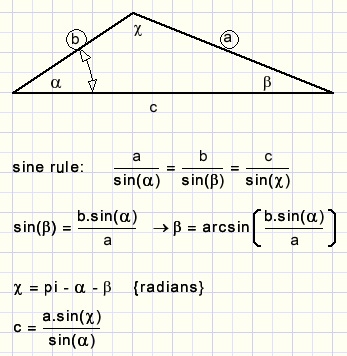
Bovenstaande procedure wordt twee maal aangeroepen om eerst AC en daarna AB te berekenen.
Dit is de procedure die a benadert:

procedure TForm1.Button1Click(Sender: TObject);
var amin,amax,angle,ha : double;
    A1,A2,A3 : TG3;
    x1,y1,x2,y2,x3,y3 : word;
    steps : byte;
begin
 amin := 0; amax := 60; //degrees
 steps := 0;
 with A1 do
  begin
   a := 4; b := 3;
  end;
 with A2 do
  begin
   a := 5; b := 4;
  end;
 with A3 do
  begin
   a := 3; b := 5;
  end;
 repeat
  inc(steps);
  angle := (amin + amax)/2;
  A1.alpha := angle*deg2rad;
  triangle(A1);
  A2.alpha := (60*deg2rad-A1.beta);
  triangle(A2);
  if A1.c < A2.c then amax := angle else amin := angle;
 until abs(A1.c - A2.c) < 1e-6;
 statictext1.Caption := formatfloat('##0.00000',A1.c);
 statictext2.caption := formatfloat('##0.000',angle);
 statictext3.caption := inttostr(steps);
//
 x1 := 300;
 y1 := 150;
 with paintbox1 do with Canvas do
  begin
   brush.Color := $ffffff;
   brush.style := bsSolid;
   fillrect(rect(0,0,width,height));
   pen.Width := 1;
   pen.Color := $000000;
   brush.Style := bsClear;
   ellipse(150,150,450,450);
   ellipse(100,100,500,500);
   ellipse(50,50,550,550);
   pen.Color := $ff0000;
   moveto(300,150);
   x2 := 300-round(50*A1.c*sin(A1.alpha));
   y2 := 150+round(50*A1.c*cos(A1.alpha));
   lineto(x2,y2);
   ha := 0.5*pi - A1.alpha - a1.beta - A2.alpha;
   x3 := x2 + round(50*A1.C*cos(ha));
   y3 := y2 - round(50*A1.C*sin(ha));
   lineto(x3,y3);
   lineto(x1,y1);
   pen.color := $0000ff;
   moveto(300,300);
   lineto(x1,y1);
   moveto(300,300);
   lineto(x2,y2);
   moveto(300,300);
   lineto(x3,y3);
  end;
end;

En hier (verkleind) het resultaat: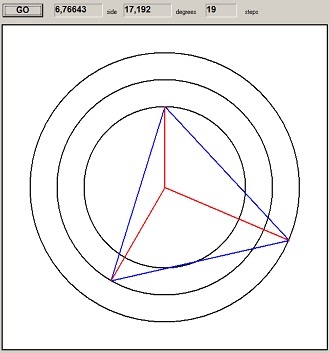

De zijde a is 6,766 lang en deze benadering vergde 19 stappen.

OneStat