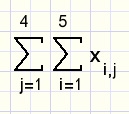| Gemiddeldes, Som- en Product notaties |  |
Constanten en Variabelen
Vaste getallen zoals, 1 , 2 of 3,89 noemen we constanten.Voor getallen die we nog niet weten schrijven we even een letter, zoals a, x, of y.
Zo'n letter noemen we een variabele.
Soms hebben we een rijtje variabelen van hetzelfde soort, zoals de aankopen in een supermarkt.
De prijs van die artikelen kunnen we natuurlijk a,b,c... noemen.
Maar één letter is handiger en om onderscheid aan te brengen plaatsen we een cijfertje iets rechtsonder.
Dat cijfertje heet de index.
Een variabele met een index heet een geïndexeerde variabele.
Voor drie variabelen x krijgen we dan x1, x2, x3 ....
De Somnotatie
De som x1 + x2 + x3 schrijven we korter als
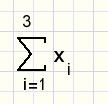
i is hier de index, die neemt achtereenvolgens de waarden 1,2,3, aan.
Onder het sigma teken staat de index met zijn beginwaarde,
boven het sigma teken staat de eindwaarde van de index.
Een paar voorbeelden van somnotaties:
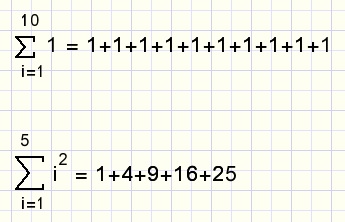
De Productnotatie
Wat voor de som kan is natuurlijk ook voor een product mogelijk.
Het product x1 . x2 . x3 schrijven we korter als
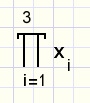
Het Rekenkundig gemiddelde
Het rekenkundig gemiddelde wordt verkregen door een rijtje getallen op te tellen
en de som door het aantal te delen.
Voorbeeld:
We kopen vijf Sinterklaascadeautjes van €12, €9, €22, €40 en €17.
Dat is totaal voor €100.
De gemiddelde prijs van een cadeau was dus 100/5 = €20.
Somnotatie van een rekenkundig gemiddelde van n getallen:
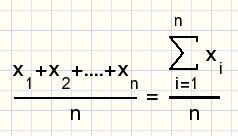
Het Meetkundig gemiddelde
Dat gemiddelde verkrijgen we door de getallen met elkaar te vermenigvuldigen en
uit het product de n-de machts wortel te trekken.
Voorbeeld:
Iemand ontvangt in 4 achtereenvolgende jaren 3%, 5%, 10% en 7% rendement op zijn aandelen.
Het gemiddelde rendement is dan de vierdemachts wortel uit het product 1,03 * 1,05 * 1,1 * 1,07 = 1,062
dus 6,2%.
Productnotatie van het meetkundig gemiddelde van n getallen:
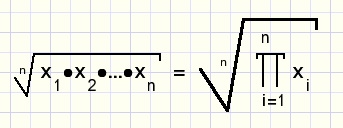
Het Harmonisch gemiddelde
Voorbeeld:
Boven een badkuip zijn twee kranen gemonteerd.
Met de ene kraan kan het bad in 15 minuten vollopen.
Met de andere kraan gaat dat in 9 minuten.
Wat is het gemiddelde van die twee kranen?
Als kraan 1 één minuut open staat dan is het bad voor 1/15 deel gevuld.
Met kraan 2 is dat 1/9 deel, dus samen open: 1/15 + 1/9 deel,
zodat het vullen met twee kranen 1/(1/15 + 1/9) = 5,625 minuten duurt.
Een zelfde prestatie was geleverd door twee gelijke kranen die elk afzonderlijk
het bad in 2*5,625 = 11,25 minuten hadden opgevuld.
Voorbeeld:
Een automobilist rijdt op de heenweg constant 100km/uur en op de terugweg 70km/uur.
Wat is de gemiddelde snelheid?
Die is natuurlijk totale afstand / totale tijd.
Stel de afstand = 1.
De heenweg duurt dan 1/100 uur, de terugweg 1/70 uur.
De gemiddelde snelheid is dan 2/(1/100 + 1/70) = 82,35km/uur.
Het harmonisch gemiddelde van n getallen:
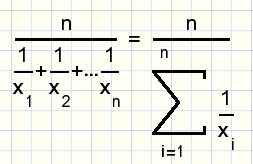
Het Kwadratisch gemiddelde
Zie hiervoor [DIT] artikel.Gewogen gemiddeldes
Klas 1a telt 30 leerlingen en klas 1b telt 20 leerlingen.in klas 1a wordt gemiddeld het cijfer 6 gescoord voor een proefwerk wiskunde.
In klas 1b is het gemddelde cijfer 7,2.
Wat is nu het gemiddelde cijfer van een leerling in de klassen 1a en 1b?
Dat is natuurlijk 30*6 + 20*7,2 en deze som dan delen door 30+20.
Die 30 en twintig noemen we wel weegfactoren
Het gewogen (rekenkundige) gemiddelde van getallen x1..xn met
weegfactoren w1..wn is:
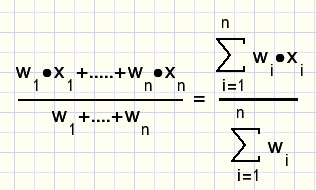
Die formule kan zonder de noemer als de weegfactoren opgeteld 1 zijn.
Voorbeeld:
Een rapportcijfer wordt bepaald door een werkstuk, schriftelijke overhoring en een proefwerk.
Die hebben opvolgend weegfactoren 0,2 0,3 en 0,5.
Een leerling met het cijfer 9 voor een werkstuk, 4 voor een overhoring en 6 voor een proefwerk
krijgt dan als rapportcijfer 0,2*9 + 0,3*4 + 0,5*6 = 6
Valkuilen
De meeste gemiddelden betreffen het rekenkundige gemiddelde en daarvoor tellen we getallen op.Als die getallen betrekking hebben op een situatie waarbij niet kan worden opgeteld, dan slaat de berekening
van het gemiddelde nergens op.
Voorbeeld:
Stel dat wij dagelijks gemiddeld 3 liter water ontvangen.
Ruim genoeg dus.
Helaas is er één week van het jaar geen water.
Zonder opslagmogelijkheid van dat water (ton, emmer) betekent dat wel onze dood.
Optellen is hier: opslag van het water.
Bij windmolens is het probleem dat het vaak niet waait.
Toch rekent men met gemiddeld 30% van de tijd waarop wel voldoende wind waait.
Maar zonder de mogelijkheid tot opslag van elektrische energie is dat gemiddelde flauwekul.
Want als het niet waait dan heb je niks.
Som van Sommen
Hieronder staat een tabel van 4 rijen en 5 kolommen.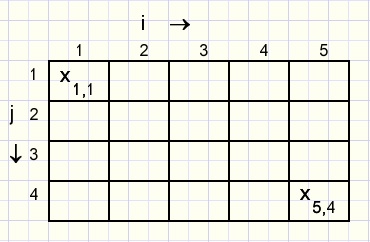
In elk vakje staat een getal x.
De x in kolom 5 van rij 4 geven we aan met twee indices x5,4.
De optelling van alle getallen voeren we uit door eerst per rij te sommeren
waarna we de rijen optellen.
Dat levert twee somtekens na elkaar op: