functies tekenen

Functies tekenen

download exerciser programma

download Delphi-7 project

bekijk source code

Dit artikel beschrijft een Delphi project voor het tekenen van functies.

De functies zijn vooraf bekend zodat er geen formules vertaald hoeven worden.
De theorie van de formule vertaling staat hier.

Dit artikel beperkt zich tot zoomen en scrollen.
Ook wordt een methode uitgelegd om asymptoten en floating point exceptions te herkennen.

Het coördinatenstelsel

Doel van een (2D) coördinatenstelsel is het aangeven van de posities van punten.
Hiervoor trekken we twee lijnen die loodrecht op elkaar staan.
De horizontale lijn noemen we de X-as, de vertikale lijn de Y-as.
De positie van een punt P geven we aan met P(x,y) waarbij x de afstand is tot de Y-as en
y de afstand tot de X-as. (x,y) noemen we de coördinaten van P.

Van een willekeurige functie y=f(x) is x de onafhankelijke variable,
y is de afhankelijke variabele, immers verkregen door op x een berekening los te laten.

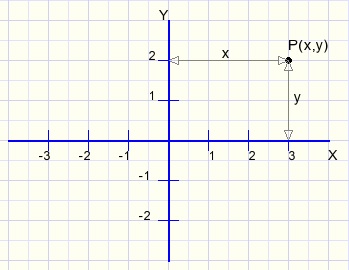
P(3,2) betekent dat punt P een afstand 3 heeft tot de Y-as en afstand 2 tot de X-as.
Het snijpunt van de assen heeft de coördinaten (0,0).

De variabelen X en Y gebruiken we als de context onbekend is.
In andere gevallen is x bijvoorbeeld de tijd (seconden, uren..) en y de temperatuur, waterhoogte of afstand.

Dit Delphi project gebruikt een paintbox om het coördinatenstelsel weer te geven.
Tekenen gebeurt direct in deze paintbox, hieronder verkleind afgebeeld:

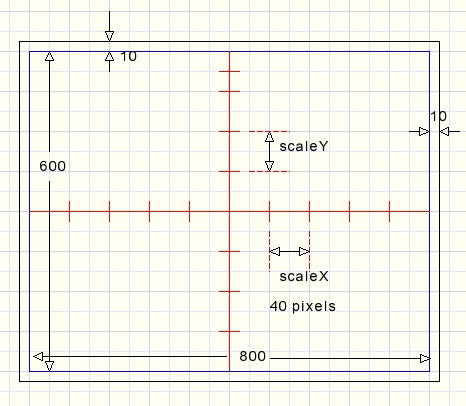
De breedte is 800 pixels plus 10 pixels ruimte aan de linker- en rechterkant.
De hoogte is 640 pixels plus 10 pixels ruimte aan de boven- en onderkant.
De rasterlijnen staan op 40 pixels afstand van elkaar.
De X en Y assen zijn rood getekend.

Een belangrijke pixel is (410,330) : het midden van de paintbox.
Zoomen en scrollen geschiedt relatief ten opzichte van dit midden.

De volgende constanten en variabelen beschrijven het coördinatenstelsel:

const maxscalecode = 9;
      minscalecode = 0;
      maxCenter     = 1000;
      minCenter     = -1000;
      scalesBase : array[0..2] of single = (1, 2, 5);
      scalesExp  : array[0..3] of single = (0.01, 0.1, 1, 10);

var centerX : single = 0;
    centerY : single = 0;
    scaleX  : single = 1;
    scaleY  : single = 1;
    scaleCodeX : byte = 6;
    scaleCodeY : byte = 6;
    timercode : byte = 0;
    formulaNr : byte = 1;

scaleX,scaleY is de afstand tussen de vertikale en horizontale rasterlijnen,
dus de lengte van 40 pixels.
De default schaal is 1.
Linker- en rechter muiskliks in een statictext component veranderen de schaal.
Scalecodes zijn handig omdat ze verhoogd en verlaagd kunnen worden.

De scalecodes geven de volgende schaal:

scalecode		scale
0		0.01
1		0.02
2		0.05
3		0.1
4		0.2
5		0.5
6		1
7		2
8		5
9		10

centerX, centerY zijn de coördinaten van het middelste pixel van de paintbox.
Ook deze waardes kunen gewijzigd worden met muiskliks op de betreffende static text component.
CenterX, centerY zijn altijd veelvouden van de schaal.

Deze procedure berekent de schaal uit de scalecode:

procedure scalecode2scales;
// scaleCode = scaleBaseIndex + 3*scalesExpIndex
var i,j: byte;
begin
 i := scalecodeX mod 3;
 j := scalecodeX div 3;
 scaleX := scalesBase[i] * scalesExp[j];
 centerX := round(centerX/scaleX) * scaleX;  //make center multiple of scale
 i := scaleCodeY mod 3;
 j := scaleCodeY div 3;
 scaleY := scalesBase[i] * scalesExp[j];
 centerY := round(centerY/scaleY) * scaleY;  //make center multiple of scale
end;

De schaal veranderen heet zoomen, de center waardes veranderen is scrollen.

Functies plotten: de basis methode

Als y = f(x) dan kan y worden berekend voor elke waarde van x.
Die berekeningen leveren een aantal getallenparen (x,y)
op die als punten in een coördinatenstelesel getekend kunnen worden.
Zo is in één oogopslag de functie te zien.

Stel dat we y=f(x) berekenen voor x=0, x=0,5 x=1 enzovoorts.
Laten we de waarden van x x1,x2,x3...noemen en de bijbehorende waarden van y y1,y2,y3...
Eerst zetten we de (canvas) pen op (x1,y1) en dan trekken we een rechte lijn naar (x2,y2)
dan een rechte lijn naar (x3,y3) enzovoorts.
Maar bij het tekenen hebben we te maken met pixels, niet coördinaten.
Er moet dus een vertaling plaatsvinden van pixel naar coördinaat en omgekeerd.

Beginnend met horizontale pixelpositie 10 berekenen we de waarde van X
met behulp van de schaal en de waarde van het centrum.
Met deze X waarde berekenen we de functiewaarde Y.
Met Y berekenen we de vertikale pixelpositie, waarna we de pen op het pixel kunnen plaatsen.
De procedure wordt herhaald voor pixel 11,12....en we trekken lijnen van punt naar punt.

Deze functie berekent de X waarde uit het horizontale pixel positie:

function pix2X(px : smallInt) : single;
//pixel value px to x value
begin
 result := centerX+0.025*(px-410)*scaleX;
end;

Deze functie zet de functiewaarde Y om naar de vertikale pixel positie:

function getPixelValue(y : single) : smallInt;
var pixY : single;
begin
 PixY := 330 - 40*(y-centerY)/scaleY;
 if PixY < 0 then pixY := -1;       //avoid integer overflowing
 if PixY >= 660 then PixY := 660;
 result := round(PixY);
end;

Merk op dat eerst een floating point waarde wordt berekend.
Daarmee voorkomen we een integer overflow, wat bij grote schaal zou leiden tot rare vertikale strepen.
Nu kunnen we al heel wat functies tekenen maar lang niet alle.

Floating Point exceptions

Sommige floating point berekeningen leveren fouten op.
Delen door nul en de wortel trekken uit een negatief getal zijn de meest voorkomende gevallen.
Wat te doen als dit optreedt?
Het antwoord is simpel: niets.
We mogen alleen lijnen trekken tussen punten die foutloos zijn berekend.
Daarom levert de berekening van de functiewaarde ook een (boolean) vlaggetje (v)
dat aangeeft of de berekening is gelukt.

Alleen als v true is dan mogen we de pen neerzetten of een lijn trekken.
Wat we moeten doen bepaalt de variable plotcode

Plotcode=1 zet de pen neer.
Plotcode=3 tekent een lijn.

Deze functie berekent de waarde van de geselecteerde functie:

function getValue(x : single; var v : boolean) : single;
//calculate function value
var sqx : single;
begin
 result := 0;
 try
  case formulaNr of
   1 : result := 0.1*x*x-6;
   2 : result := sqrt(64-sqr(x));
   3 : begin
        sqx := x*x;
        result := sqx*(-0.01*sqx +0.5);
       end;
   4 : result := 1/(x-2.001);
   5 : result := 5/((x-4.001)*(x+3.999));
  end;//case
  v := true;
 except
  v := false;
 end;
end;

Deze (vereenvoudige) code verzorgt het tekenwerk:

var px,py : smallInt;
    x,y : single;
    plotcode: byte;
    valid : boolean;		
begin	
with form1.plotbox.canvas do
............
 for px := 10 to 809 do
  begin
   X := pix2X(px);
   Y := getValue(x,valid);
   if valid then py := getPixelvalue(y);
   plotcode := (plotcode shl 1) and $3;
   if valid then plotcode := plotcode or $1;
   with form1.plotbox.Canvas do
    case plotcode of
     1 : MoveTo(px,py);
     3 : lineto(px,py);
   end;//case
  end; //for px

Asymptoten

Tenslotte is er nog een valkuil.
Neem de functie y = 1/x
Voor x = -0.001 y = -1000.
Voor x = 0.001 y = 1000.
De lijn line x = 0 noemen we een asymptoot.
Die willen we niet tekenen want de punten horen niet bij de functie.
Als asympoten samenvallen met het raster dan ontstaat vanzelf een floating point fout (delen door nul)
de V vlag wordt false en de asymptoot wordt niet getekend.
De functie y = 1/(x-0.01) heeft als asymptoot x = 0.01
Bij een horizontale schaal van 1 (0.025 per pixel), gebeurt er dit:

Zonder extra test trekken we de lijn van (0, -100) naar (0.025, 66.67) wat niet de bedoeling is.

Wat nu?
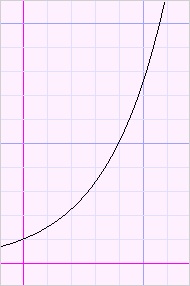
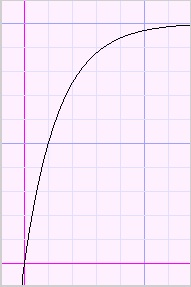
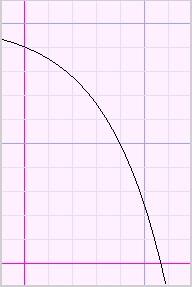
Kijk eens naar de grafieken hieronder:


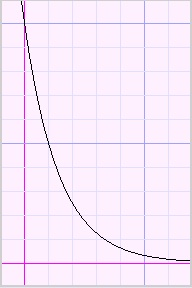toenemende stijging	afnemende stijging	toenemende daling	afnemende daling

We zien stijging en daling, toenemend of afnemend.

Dit gedrag blijkt uit de eerste en tweede afgeleiden van de functie.
Tussen twee opvolgende pixels (x1,y1) en (x2,y2) is de eerste afgeleide: (y2-y1)/(x2-x1).

Bekijk nu eens drie opvolgende pixels (x1,y1) (x2,y2) en (x3,y3).
Omdat steeds de horizontale stapjes gelijk zijn stellen we die even gelijk 1,
De eerste afgeleiden worden dan (y2-y1) en (y3-y2).
Voor toenemende functies is de eerste afgeleide positief,
voor afnemende functies is die negatief.

De tweede afgeleide is het verschil tussen opvolgende eerste afgeleiden: (y3-y2) - (y2-y1).
Bij toenemende stijging is ook de tweede afgeleide positief.
Bij afnemende stijging is echter de tweede afgeleide negatief.

Nu komt de truuk.
We berekenen voor drie opvolgende punten de Y waarden.
Als de eerste afgeleiden hetzelfde teken hebbe dat tekenen we de lijnen tussen die punten.
Dan hebben we te maken met stijgende af dalende functies.
Maar als bij een nieuw (vierde) punt de afgeleide van teken verschilt met het vorige punt
dan bekijken we de tweede afgeleide van de vorige drie punten.
Zijn de tekens van die eerste- en tweede afgeleiden ongelijk, dan tekenen we de lijn niet.
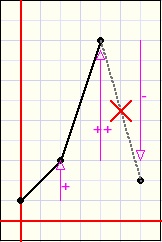
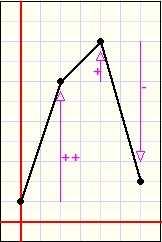
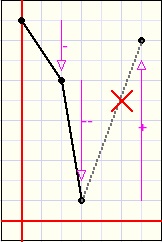
De plaatjes hierna laten zien wat we doen:


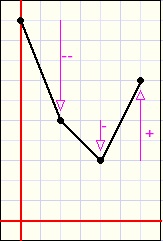niet tekenen	OK	niet tekenen	OK

We tekenen geen daling direct na een toenemende stijging en
ook geen stijging na een toenemende daling.
Hieronder staat tenslotte de volledige teken procedure:

procedure TForm1.plotbtnClick(Sender: TObject);
var x,y,prevY,dY,prevdY,ddY : single;
    valid,OK : boolean;
    plotcode : byte;
    px,py : smallInt;
begin
 plotcode := 0;
 py := 0;
 prevY := 0; prevdY := 0; ddY := 0;
 with form1.plotbox.Canvas do
  begin
   pen.Color := $000000;
   pen.Width := 1;
  end;
 for px := 10 to 809 do
  begin
   X := pix2X(px);
   Y := getValue(x,valid);
   if valid then py := getPixelvalue(y);
   dy := Y-prevY;
   if dY*prevdY >= 0 then OK := true        //asymptote suppression
    else OK := dy*ddy >= 0;
//   OK := true;                            //OK=true allows drawing asymptotes
   valid := valid and OK;
   plotcode := (plotcode shl 1) and $3;
   if valid then plotcode := plotcode or $1;
   with form1.plotbox.Canvas do
    case plotcode of
     1 : MoveTo(px,py);
     3 : lineto(px,py);
   end;//case
   ddY := dY - prevdY;
   prevdY := dY;
   prevY := Y;
  end; //for px
end;

Y		functie waarde van het laatste punt.
prevY		functie waarde van het vorige punt.
dY		afgeleide Y-prevY.
prevdY		vorige afgeleide.
ddY		tweede afgeleide dY-prevdY.

Tot zover deze beschrijving.