De Rangorde van een Breuk
download
programma		 download hele
Delphi-7 project

Theorie

Het is mogelijk aan elke breuk een uniek geheel getal te koppelen (rangorde of rank).
Dit is de truuk:
    Als t / n een niet vereenvoudigbare breuk is dan kunnen er twee andere breuken van worden afgeleid,
    genaamd het left- en right child.
    Zie het plaatje hieronder:

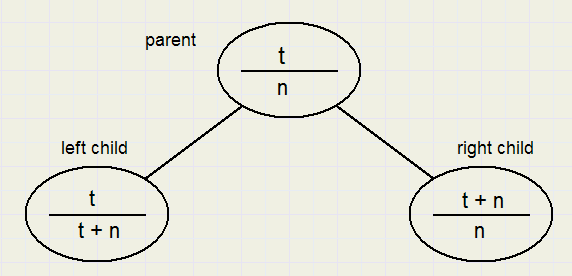
Beginnend met 1/1 aan de top komen zo alle breuken aan bod.
Van belang is dat
    - geen breuk wordt overgeslagen
    - geen breuk meer dan eens voorkomt
    - breuken niet vereenvoudigbaar zijn (dus geen gemeenschappelijke factor bevatten)
Die eisen zijn eenvoudig te bewijzen met tegenspraak.
Ook valt op, dat het proces sterk lijkt op het theorema van Euclides om de GGD van twee getallen te berekenen.

Hieronder staan de eerste resultaten
Elke breuk heeft een code van bits.
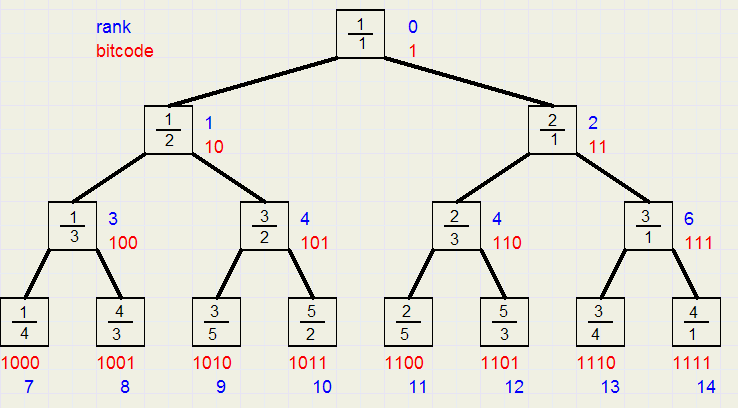
Beginnend met code 1 aan de top voegt het left-child een "0" toe aan de code van de parent,
het right-child voegt een "1" toe .
Om met een rangorde van 0 te beginnen, is de rangorde van een breuk simpelwegzijn code verminderd met 1.

In het plaatje hierboven is de bitcode in rood en de rangorde in blauw weergegeven.

Het programma

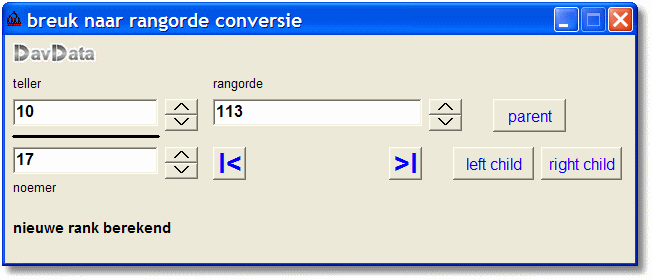
Een programma berekent bij elke breuk de rangorde en omgekeerd.
De kleinste breuk is 1/63 en de hoogste 63/1.
Edit velden voor de teller, de noemer en de rangorde maken wijziging mogelijk.
Als een veld verandert worden de andere aangepast.
Speedbuttons zorgen voor verhogen of verlagen van elk veld.
Ook is het mogelijk door de binaire boom te navigeren met de parent en child knoppen.