Floating point formaten

Floating Point getallen onderzoeken

download het test programma

download het gehele Delphi-7 project

bekijk de source code

Inleiding

In dit artikel onderzoeken we de IEEE floating point notatie van Intel.
Klik bovenaan deze pagina op het bliksem icoontje om het demonstratieprogramma te downloaden.
Dit programma toont van een floating point getal bit voor bit de interne representatie.

Hieronder staat een afbeelding van het programma:

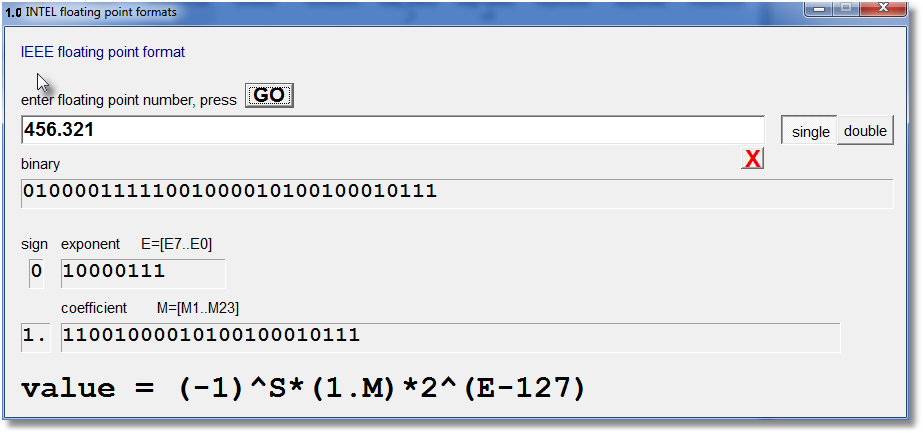
Floating point: de wetenschappelijke notatie

Floating point getallen zijn getallen met een komma (punt in het Engels)
Voorbeelden zijn:

In de "wetenschappelijke notatie", zijn getallen geschreven met één cijfer voor de komma, de rest erachter.
Een macht van 10 wordt dan toegevoegd voor de correcte waarde.
Dus

^-1

In het tweetallig stelsel heeft een getal in wetenschappelijke notatie de vorm: 1.xxxxxxx * 2^yyyy
x...x is de mantisse, y...y is de exponent.
In het IEEE floating point formaat wordt de "1" voor de komma niet weergegeven, maar alleen intern toegevoegd.

De IEEE standaard bewaart floating point getallen in de wetenschappelijke notatie.
Er zijn twee formaten:

32 bit

De decimale komma (of .) staat links van M₁.
Bit M_n representeert de waarde 2^-n
De M bits samen zijn de "mantisse".
Merk op: M₀ = 1

Bit 31 is het teken bit van de mantisse.
Indien "1" is de mantisse is negatief, indien "0" is de mantisse positief.

Bits E₇ .. E₀ vormen de exponent, die is de macht van grondtal twee.
Een bias (voorinstelling) van 127 (binair 01111111) wordt toegepast,
een exponent gelijk 0 wordt geschreven als 01111111.
De reden hiervoor is simpeler vergelijking van getallen.

Voorbeelden

1.
getal 8 = 1000 binair
Wetenschappelijke notatie: 1.00000000 * 2³
mantisse = 0 (1. niet weergegeven)
exponent = 3, met bias 127 + 3 = 130 = 10000010 binary
Tekenbit = 0

floatingpoint getal:

0 10000010 00000000000000000000000
2.
getal 1/8 = 0.125 = 0.001 binair.
Wetenschappelijke notatie: 1.000000 * 2^-3
exponent = -3, met bias 127 - 3 = 124 = 01111100 binair
Tekenbit = 0

floating point getal:

0 01111100 00000000000000000000000 3.
getal 48.7 = 110000.101100110011001101
Wetenschappelijke notatie: 1.10000101100110011001101 * 2⁵
exponent = 5, met bias 127 + 5 = 132 = 10000100 binair.
Tekenbit = 0

floating point getal:

0 10000100 10000101100110011001101

Waarom een bias in de exponent?

Stel, we vergelijken getallen 1 en 1/2
Voor de eenvoud van de uitleg gebruiken we even floating point getallen met
exponent en mantisse van slechts 4 bits.

Zonder bias:

    1 .... 0000 [1] 0000
    1/2... 1111 [1] 0000

Opmerking: 1111 (binair) is -1 (decimaal) in 2 complement notatie.
Bij vergelijking als gehele getallen concluderen we dat 1/2 > 1, maar dat is fout.

Maar met bias (van 0111)

    1 .... 0111 [1] 0000
    1/2... 0110 [1] 0000

Nu levert de vergelijking van 1 en 1/2 op dat 1/2 < 1 wat correct is.

De exponent bias bespaart circuits.
Floating point getallen kunnen als gehele getallen worden vergeleken.

Het 64 bit formaat

De mantisse is 52 bits groot. (plus 1.)
Opnieuw is M₀ = 1 , niet weergegeven maar alleen inwendig aan berekeningen toegevoegd.
De exponent bias is 01111111111
Bit 63 is het tekenbit van de mantisse.

Algemeen: getallen naar een ander talstelsel omrekenen

Stel we hebben twee getallen met dezelfde waarde maar geschreven in verschillende talstelsels:

    aaaa,bbbb
    cccc,dddd

Die getallen kunnen alleen gelijk zijn als geldt: aaaa = cccc (het gehele deel) en bbbb = dddd (het komma deel)
Bij omrekening moeten het gehele- en het kommadeel apart worden omgezet.

Omzetting van decimaal naar binair (gehele deel)

We starten met dezelfde getallen dddd (decimal) and bbbb (binair)
Deling door 2: bbbb / 2 = bbb,b ..... het rechter cijfer achter de komma is de rest.
Dus geldt ook: dddd / 2 = ddd,b
Conversie vindt plaats door herhaald delen door 2 en bewaren van de resten.
We converteren 841 naar binair:

    841 / 2 = 420 r 1
    420 / 2 = 210 r 0
    210 / 2 = 105 r 0
    105 / 2 =  52 r 1
     52 / 2 =  26 r 0
     26 / 2 =  13 r 0
     13 / 2 =   6 r 1
      6 / 2 =   3 r 0
      3 / 2 =   1 r 1
      1 / 2 =   0 r 1

Dus [841]₁₀ = [1101001001]₂

Omzetting van decimaal naar binair (kommadeel)

Bekijk dezelfde getallen 0,dddd en 0,bbbb
Vermenigvuldigen met twee: 0,bbbb * 2 = b,bbbb

Het meest linkse cijfer plopt eruit voor de komma.
Conversie is dus hehaald vermenigvuldigen met 2 en het gehele cijfer opslaan.
We rekenen .841 om naar binair:

     .841 * 2 = 1.682
     .682 * 2 = 1.364
     .364 * 2 = 0.728
     .728 * 2 = 1.456
     .456 * 2 = 0.912
     .912 * 2 = 1.824
     .824 * 2 = 1.648

Dus [.841]₁₀ = [.1101011 ]₂ Dit is wel een benadering, meer cijfers geven meer nauwkeurigheid.
Opmerking: 0,1 decimaal kan binair niet exact worden weergegeven, het blijft altijd een benadering.

Omzetting van binair naar decimaal

In het tweetallige getal b₃ b₂ b₂ b₀ . b_-1 b_-2 b_-3

heeft een cijfer b_n de waarde 2ⁿ
Binair 101.011 naar decimaal omzetten:

  1--.--- = 4
  -0-.--- = 0
  --1.--- = 1
  ---.0-- = 0
  ---.-1- = 0.25
  ---.--1 = 0.125
  ================
 total      5.375

Hoe werkt het programma?

De geheugenlocatie waarop het floating point getal staat wordt geadresseerd als array van bytes.
Dan worden individuele bits uit het array geplukt en in character string s geplaatst.

Opmerking: array byte[0] staat in bits 0..7 van het 32 bit memory word.

type TA = array[0..7] of byte;
     PA = ^TA;

4 bytes zijn nodig voor 32 bits, 8 bytes zijn nodig voor een 64 bit floating point getal.
De PA pointer type wijst naar een byte array.
In geval van het 32 bit formaat:

var p : PA;
    i,j : byte;
    s,t : string;
    f32 : single;
begin
 s := '';
 try
  f32 := strtofloat(form1.number.text);
  p := PA(@f32);
  for j := 3 downto 0 do
   for i := 7 downto 0 do s := s + chr(((p^[j] shr i) and 1) + ord('0'));
  sign.Caption := s[1];
  t := '';
  for i := 2 to 9 do t := t + s[i];
  exponent.Caption := t;
  t := '';
  for i := 10 to 32 do t := t + s[i];
  coef.Caption := t;
 exept
  ......
 end;

Hiermee eindig ik deze beschrijving van floating point getallen.