Het flippo probleem

Download (Windows) programma
Download Delphi(7) project

Inleiding

Flippo's zijn kleine ronde kartonnen of kunststof schijfjes met daarop een afbeelding.
Ze werden door chipsfabrikant Smith aan de zakjes toegevoegd en
waren in de jaren '90 een rage.

Zo kon de consument series verzamelen van voetballers, filmsterren of stripfiguren.

Het probleem is nu:
Wat is de kans op een complete serie gegeven het aantal verzamelde flippos?
In dit artikel geef ik drie methoden van berekening.
De basiskennis hiervoor is te vinden in de cursus combinatoriek

Een computerprogramma past alle methoden toe.

De flippos in een verzameling noem ik 1,2,3,...N
waarbij N het aantal flippos is van een volledige serie.
K is het aantal verzamelde flippos.

De tel methode

We schrijven simpelweg alle rijtjes met lengte K op die er zijn te leggen en
tellen dan het aantal rijtjes dat een volledige verzameling bevat.

Stel N=3 en K=5, dan zien die 35 = 234 rijtjes er zo uit
    1 1 1 1 1
    1 1 1 1 2
    ...
    1 3 3 3 3
    2 1 1 1 1
    ...
    3 3 3 3 3
Een goed rijtje is dan bijvoorbeeld: 3 3 1 1 2
een fout rijtje : 2 2 1 1 2

Een computerprogramma telt het aantal goede rijtjes, stel dit aantal G.
Het totale aantal rijtjes is NK, want we kiezen K maal uit N flippos.
De kans op een hele serie is dan (goede uitkomsten gedeeld door totaal mogelijke uitkomsten)



Deze methode kost veel tijd zodat we ons moeten beperken tot kleine aantallen N en K {NK < 250.000.000}

Een formule

Stel A(1) het aantal rijtjes waarin flippo 1 absent is.
Dan moeten we K maal kiezen uit (N-1) flippos, dus zijn er maar (N-1)K van zulke rijtjes te leggen.
Stel A(1+2) is het aantal rijtjes waarin flippos 1 OF 2 ontbreken en
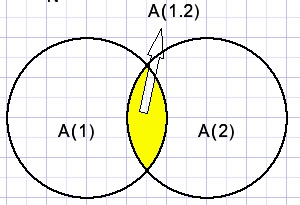
A(1.2) het aantal waarin 1 EN 2 niet voorkomen.
Lees "+" als OF en "." als EN.
Dan is A(1+2) = A(1) + A(2) - A(1.2) de laatste term corrigeert dubbeltelling.



Zo is ook:
A(1+2+3) = A((1+2)+3) = A(1+2) + A(3) - A((1+2).3)
A((1+2).3) = A(1.3+2.3) = A(1.3) + A(2.3) - A(1.2.3)

Deze rekenregels zijn in te zien door overlappende vlakken te tekenen zoals in de figuur hierboven.

Combinerend:
A(1+2+3) = A(1) + A(2) + A(3) - [A(1.2 + A(1.3) + A(2.3)] + A(1.2.3)

A(1) = A(2) = ..= A(K) zijn N termen.
A(1.2) = A(1.3) = A(2.3) = .... = A((k-1),K) zijn net zoveel termen als er combinaties zijn van 2 uit N.

Dat leidt tot de formule voor het aantal incomplete rijtjes:



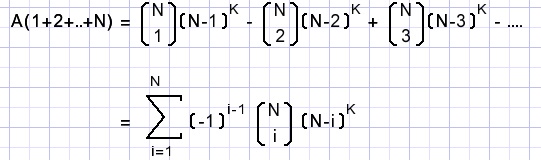
Het aantal wel complete rijtjes is dan NK - A(1+2+..+N)
Dit verschil delen door NK levert de kans op een hele serie bij aankoop van K zakjes chips.

Het computerprogramma kan ook deze formule gebruiken.

Een kortere formule

Nu een eenvoudige formule die alleen bij grote aantallen (K veelvoud van N) een goede benadering geeft
van de kans op een complete serie.

We kiezen een rij van K flippos lang zonder element 1.
De kans daarop is



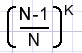
En de kans op minstens 1 flippo type 1 is



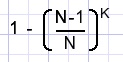
Dit herhalen we voor flippos typen 2..N zodat de kans op een complete serie is



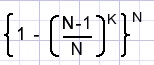
Hier vermenigvuldigen we kansen die niet helemaal onafhankelijk zijn, wat een fout oplevert.
Maar bij grote waarden van K is de fout klein.
Deze formule kan nog wat bijgeschaafd worden:



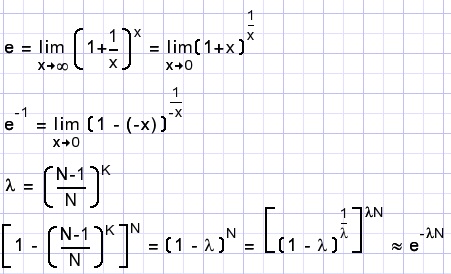
onderstaande tabel toont enkele waarden voor N = 5:

    Kformulee macht
    53,8%19,4%
    1052,5%58,5%
    2094,3%94,4%

Het programma




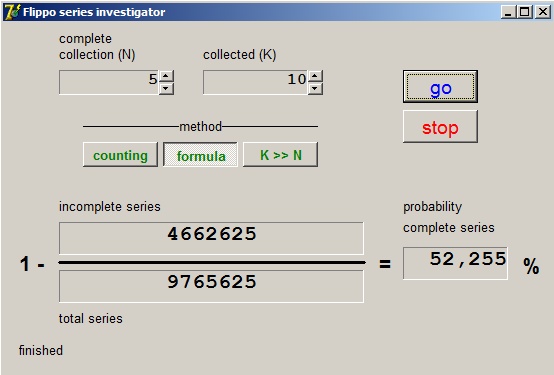
Download het programma door op het bliksem icoontje bovenaan deze pagina te klikken.