

| Ontbinden in factoren en GGD |  |
Dit programma onbindt getallen in factoren en berekent de GGD (grootste gemeenschappelijke deler).
Opmerking: GGD(A,B) * KGV(A,B) = A*B.......{KGV = kleinste gemeenschappelijke veelvoud}
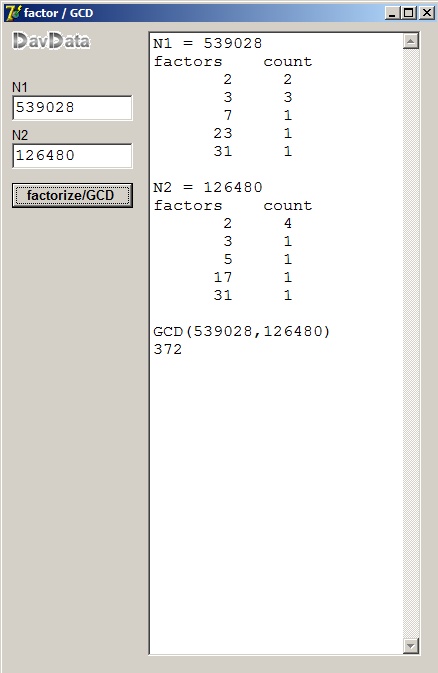
Opmerking: GCD (greatest common divisor) is Engels voor GGD.
Factoren
Factoren kan je beschouwen als de bouwstenen van getallen.Een getal in factoren ontbinden betekent dat getal schrijven als product van priemgetallen.
Voorbeeld: 3960 = 23.32.5.11
Als een hoeveelheid geschreven kan worden als product van (priem) getallen betekent dat
dat er gelijke stapeltjes zijn te maken.
Zie het plaatje hieronder waar de hoeveelheid 6 als 2 stapeltjes van 3 of 3 van 2 kan worden neergelegd.
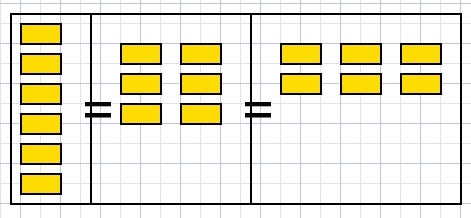
Zulke stapeltjes zijn niet mogelijk voor een priemgetal.
Wisselen van bankbiljetten is een toepassing van ontbinden in factoren in het echte leven.
Een breuk vereenvoudigen door teller en noemer te delen door de gemeenschappeijke factoren
is een andere toepassing.
Het product van de gemeenschappelijke factoren van getallen A en B schrijven we als GGD(A,B).
KGV(A,B) is het kleinste getal dat zowel door A als door B deelbaar is.
GGD(A,B)*KGV(A,B) = A*B
Probleem 1
Een supermarkt heeft 255 sinaasappelen en 595 appels en wil daar zoveel mogelijk gelijke pakketten van samenstellen.
Nu is GGD(255,595)= 85 zodat 85(3 + 7 ) het antwoord is: 85 pakketten met elk 3 sinaasappels en 7 appels.
Probleem 2
Een lichtstraal weerkaatst in een kamer met spiegelwanden.
Welke afstand legt het licht af voordat het terug is bij lichtbron A?
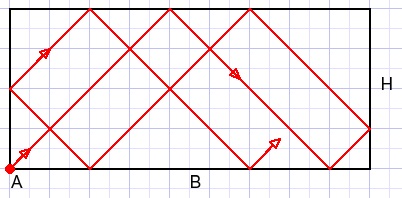
Bekijk de horizontale en vertikale afstand apart van elkaar.
Na vertikale verplaatsing 2H is de lichtstraal weer onderaan.
Na 2B verplaatsing horizontaal is de straal aan de linkerzijde.
Punt A wordt bereikt na afstand KGV(2B,2H).
In bovenstaand plaatje waar B=9 ; H=4
KGV(18,8) = 72. Dat is zowel de horizontale- als vertikale afstand.
De echte afstand is 72*(wortel uit 2).
Het programma
De kleinste priemgetallen zijn 2 en 3.Grotere priemgetallen hebben het formaat 6K-1 of 6K+1 waarbij K=1,2,3,Ö
omdat 6K,6K+2,6K+3,6K+4 geen priemgetal kan zijn.
In factoren ontbinden van een getal (N) geschiedt door te delen door alle priemgetallen
en te tellen hoe vaak de deling mogelijk is (rest is 0).
Na deling door de factoren 2,3,5 hoogt de deler afwisselend op met 2 en 4 (van 6K-1 naar 6K+1 naar 6K+5).
Dat scheelt tijd.
Een andere manier om tijd te besparen is deze:
N = Q.d + r {N: getal; d: deler; Q: quotient; r: rest}
Als Q <= d dan zullen geen nieuwe factoren worden gevonden.
Want, als f een factor is van N dan geldt: N = Q*f en f was al gevonden toen f < Q.
In het programma vervult de exit flag (XF) de taak om het programma te beŽindigen als Q <= d.
procedure factorize(N : dword);
var N1 : dword;
count : byte; //same factors
factor,m : word;
fplus : byte;
XF : boolean;
begin
factor := 2;
fplus := 2;
repeat
count := 0;
repeat
m := N mod factor;
N1 := N div factor;
XF := N1 <= factor;
if m = 0 then
begin
N := N1;
inc(count);
end;
until m > 0;
if count > 0 then report(factor,count);
if factor < 5 then factor := (factor shl 1) - 1
else begin
factor := factor + fplus;
fplus := 6 - fplus;
end;
until XF;
if N > 1 then report(N,1);
end;
De report procedure voegt de factor toe aan een Tmemo component.De GGD van twee getallen is te verkrijgen door vermenigvuldigen van hun gemeenschappelijke factoren
maar er is een simpeler methode: het theorema van Euclides.
Euclides
Het theorema van Euclides komt neer op GGD(A,B) = GGD(A-B,B) waar geldt: A>B.
function GCD(A,B : dword) : dword;
var H : dword;
begin
while A > 0 do
begin
if A < B then begin
H := A;
A := B;
B := H;
end;
A := A mod B;
end;
result := B;
end;
Voor details verwijs ik naar de source code.

