download
Euclides		 de oplossing van Ax + By = C

Inleiding
In dit artikel wordt beschreven hoe mijn programma "Euclides" x en y oplost in de vergelijking Ax + By = C,
waarbij A,B,C,x,y gehele getallen zijn.
Dit type hoort tot de Diophantische vergelijkingen.

Download het programma door op het download (bliksem) logo bovenaan deze pagina te klikken.

Dit soort vergelijkingen ontstaat bijvoorbeeld uit de puzzel:

    Een verzamelaar van antieke auto's laat zijn vier kinderen het volgende testament na:

    Jan: 40% van de wagens is voor jou. Schenk 5 andere aan een museum.
    Heleen: 40% van de overgebleven wagens is voor jou. Schenk 3 andere aan een museum.
    Emiel: 40% van de overgebleven wagens is voor jou. Schenk 1 andere aan een museum.
    Roderick : de resterende wagens zijn voor jou.
Vraag: uit hoeveel auto's moet de verzameling minimaal bestaan om deze verdeling mogelijk te maken?

als de verzameling uit x voeruigen bestaat, dan moet:
    0.6(0.6(0.6x - 5) - 3) - 1 een positief geheel getal zijn.
Als nu Roderick y auto's krijgt, dan:
    0.216x - 4.6 = y
    216x - 1000y = 4600
Dus moeten positieve getallen x en y worden gevonden die bovenstaande vergelijking kloppend maken.

De kern van de oplossing is het gebruik van het theorema van Euclides.
Dat behandelen we dus eerst.
Daarna zullen we zien hoe het theorema wordt toegepast om de oplossing te berekenen.

Het theorema van Euclides
Uit de losse pols komt het theorema van Euclides hierop neer:
    ggd(A,B) = ggd(A - B,B) waarin ggd betekent "grootste gemeenschappelijke deler"
In woorden:
    inplaats van te berekenen ggd(56,35), geeft ggd(56-35,35) = ggd(21,35) dezelfde uitkomst.
herhaald toegepast:
ggd(56,35) = ggd(21,35) = ggd(35,21) = ggd(14,21) = ggd(21,14) = ggd(7,14) =
ggd(14,7) = ggd(7,7) = 7.

Het bewijs bestaat uit twee onderdelen:
    1. als d een factor is van A en van B, dan is d ook een factor van A - B
    {er raakt geen gemeenschappelijke factor weg}
    2. als d een factor is van alleen A of alleen B, dan kan d geen factor zijn van A - B
    {er komt geen nieuwe factor bij}
bewijs 1.
    neem aan:
    A = ad en B = bd dan:
    A - B = ad - bd = d(a - b)
    en
    (A - B)/d = a - b wat een geheel getal is. Dus (A - B) heeft ook een factor d.

bewijs 2.
    gegeven:
    A heeft geen factor d.
    B heeft wel een factor d en B = bd
    te bewijzen:
    ggd(A-B,B) = d is niet mogelijk

    stel:
    A - B heeft een factor d, dan A - B = A - bd = kd, waarbij k een geheel getal is.
    delen door d :
    A/d - b = k
    A/d = k + b
    b en k zijn gehele getallen, A/d is een breuk, dus dit is onmogelijk.
    A - B kan nooit een factor d hebben.
Hiermee is het bewijs geleverd.

In het geval A > B levert herhaalde toepassing :
    ggd(A,B) = ggd(A - kB,B) waarin k een positief geheel getal is.
    B wordt afgetrokken van A totdat geldt: A - kB < B.
Zoals we gaan zien, lossen we met het theorema van Euclides de vergelijking op: Ax + By = 1
Daarbij is A > B en A,B zijn positief en bezitten geen gemeenschappelikjke factoren.
Met het resultaat van deze oplossing wordt dan de originele vergelijking opgelost.

De vergelijking standaardiseren.
terug naar de oorspronkelijke vergelijking 216x - 1000y = 4600

216, 1000 en 4600 bezitten een gezamenlijke factor 8. Deling door 8 vereenvoudigt de vergelijking tot :
    27x - 125y = 575
Bekijk : Ax + By = C
Als A,B,C een gezamenlijke factor bezitten, dan kan die eruit worden gedeeld om de vergelijking te versimpelen.
Vanaf dit punt nemen we aan, dat A,B en C geen gemeenschappelikke factor (meer) hebben.

Als alleen A en B een gemeenschappelijke factor hebben, bijvoorbeeld d, en A = ad, B = bd, dan
    d(ax + by) = C
    ax + by = C/d

C/d is dan een breuk maar (ax + by) is een geheel getal.
Conclusie: er is dan geen oplossing.

Vanaf dit punt nemen we aan, dat A en B geen gemeenschappelikjke factor hebben, dus ggd(A,B) = 1.

Ook nemen we aan dat in Ax + By =C
  • A > B
  • A > 0 en ook B > 0


    • 27x - 125y = 575 ..........wordt daarom veranderd in
    27x + 125y = 575........... (verander later het teken van y) en verder
    125x + 27y = 575........... (verwissel x en y later).

Algemene oplossingen
Als geldt C = 0 dan heeft Ax + By = 0 de oplossingen:

    (x = B, y = -A) of (x = -B, y = A).

stel (x1 , y1) is een oplossing van Ax + By = C
en (x0 , y0) is een oplossing van Ax + By = 0 ...............dan combinerend:

    Ax1 + By1 = C
    Ax0 + By0 = 0
    A(x1 - x0) + B(y1 - y0) = C
In het algemeen zijn dan (x1 - kB, y1 + kA) de oplossingen
waarbij k een geheel getal is dus ...-2,-1,0,1,2,3.......

Conclusie: Ax + By = C heeft geen oplossing of oneindig veel oplossingen.

Grote getallen
Terug naar 125x + 27y = 575

Eerst moet worden opgelost 125x + 27y = 1.

Als x1,y1 een oplossing is dan is x = 575x1, y = 575y1 het antwoord waar we naar zochten.

Maar deze werkwijze is niet slim, want x en y worden dan heel groot, mogelijk te groot, wat de mogelijkheden beperkt.

Het is beter om C zo dicht mogelijk bij 0 (of 1 ) te houden.
Dat kan door van C een getal A+B, A, B or (A-B) af te trekken en hiervoor x en y te corrigeren.

Inplaats van Ax + By = C lossen we op
    A(x-xcorr) + B(y-corr) = C - A.xcorr - B.ycorr
Eerst trekken we (A + B) af van C en hogen xcorr en ycorr op,
dan trekken we A van C af en verhogen xcorr, dan trekken we B van C af
en tenslotte trekken we (A-B) van C af waarna we xcorr verhogen en ycorr verlagen.
Zodoende wordt de kleinst mogelijke waarde van C verkregen.

Kijk opnieuw naar 125x + 27y = 575
27 + 125 = 152, dus 125(x-3) + 27(y-3) = 575 - 3*152 = 119
onthoud dat xcorr = 3, ycorr = 3 we lossen op 125x+ 27y = 119
trek nu 4*27 af van 119:
ycorr = 3+4 = 7 en we lossen op 125x + 27y = 119 - 4*27 = 11.
En eindelijk, als laatste stap, gebruiken we het theorema van Euclides om 125x + 27y = 1 op te lossen.
Het antwoord vermenigvuldigen we met 11 om x en y te bepalen.

Daarna moet, voor het dfinitieve antwoord, de correctie voor x en y,
de verwisseling van x en y en de tekenwisselingen worden uitgevoerd.

De oplossing van Ax + By = 1
Met het theorema van Euclides berekenen we ggd(A,B).

    A - q1B = r1
    B - q2r1 = r2
    r1 - q3r2 = r3
    r2 - q4r3 = r4
q betekent quotient, r is rest (van de deling).
Het proces stopt met r = 1, de ggd, want A en B hadden geen gemeenschappelijke factoren.

Uit het bovenstaande kunnen we het stelsel vergelijkingen schrijven: (als r4 = 1)



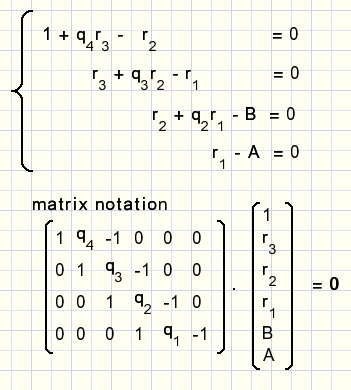
Door te "vegen" kunnen we de kolommen 2, 3, 4 op nul zetten.
Daarna ontstaat het vectorproduct:

    (
    1000-y-x
    		)(
    1
    r3
    r2
    r1
    B
    A
    		) = 0
vermenigvuldigen:
    1 - By - Ax = 0
    Ax + By = 1
Nu moeten x en y met C worden vermenigvuldigd, correcties uitgevoerd,
plus eventuele verwisseling van x en y en hun tekens.
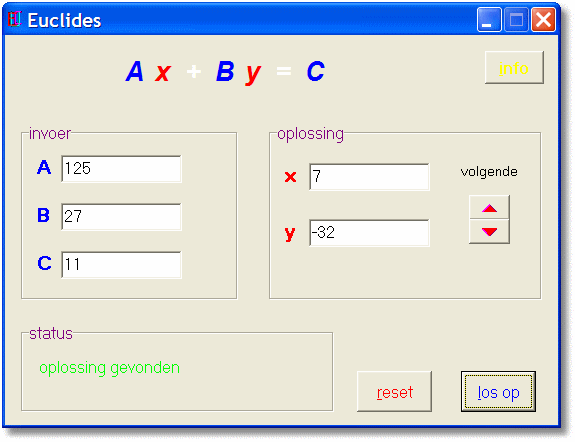
In het plaatje hierboven wordt opgelost........................125x + 27y = 11.
Om de originele vergelijking op te lossen moeten we intikken:
    A = 216...........B = -1000 ...................C = 4600
Het programma vereenvoudigt deze vergelijking naar
    A = 27..............B = -125 .....................C = 575
Daarna worden negatieve waarden van x en y getoond.
Druk op knopje "volgende" totdat een oplossing verschijnt met positieve waarden van x en y.

De uitwerking:



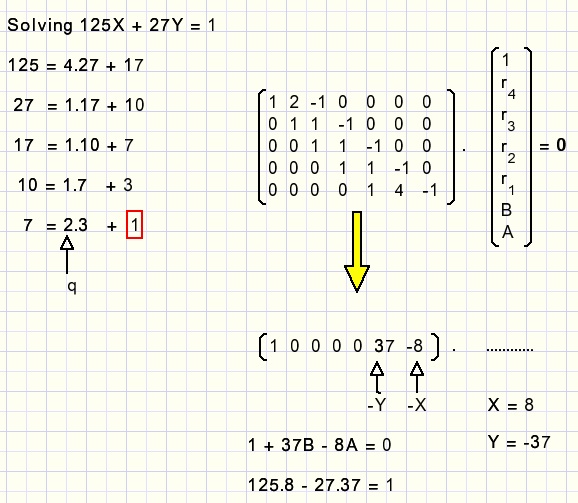
Hiermee besluit ik de beschrijving.

Hieronder staat de code voor de kern van het programma, waar Ax + By = 1 wordt opgelost.
Q[..] is een array met de quotienten van de delingen.
r is de rest van een deling.

      for i := 1 to 10 do Q[i] := 0;
  i := 0;
  repeat//calculate GCD and quotient table
   i := i + 1; 
   r := A mod B;
   Q[i] := -(A div B);
   A := B; B := r;
  until r = 0; 
  GCD := A;
  Q[i] := 1;
  if i > 2 then
   for i := i-2 downto 1 do//backward substitution
       Q[i] := Q[i+2] + Q[i+1]*Q[i];
  y := Q[1]*C+Ycorr; x := Q[2]*C+Xcorr;

Interesse in de hele source code?

Klik [hier] om het hele Delphi-3 project te downloaden.

Henrik Carlsen heeft dit project omgezet naar Delphi-10 en de stijl aangepast aan OOP
Klik [hier] om het hele Delphi-10 project te downloaden.