CRC codes

Cyclic Redundancy Checking

naar de bit calculator.

Introductie

Cyclic Redundancy Checking (CRC) is een manier om de betrouwbaarheid van gegevens te controleren.
Data kan gedurende verzending fouten oplopen door atmosferische storingen,
slechte contacten of andere defecten in apparatuur.
Beschadigde magnetische opslagmedia zorgen ook voor fouten.
Tenslotte kan data gemanipuleerd worden voor activistische doeleinden.

Het basisidee van cyclic redundancy checking (CRC) is aan de data een uniek getal te koppelen.
Dit getal wordt als volgt gemaakt:
beschouw de data (bericht M) als een lang tweetallig getal.
Kies een getal k (de key, sleutel) en deel M door k.
Die deling levert een quotient (Q) en een rest (r).
Het quotient vergeten we, dat is hier niet van belang.
De rest (r) noemen we de checksum en dit getal voegen we aan bericht M toe.

M = Q.k + r . (Message = quotient * key + rest)

Het volgende plaatje toont wat er bij verzending van het bericht plaats vindt:

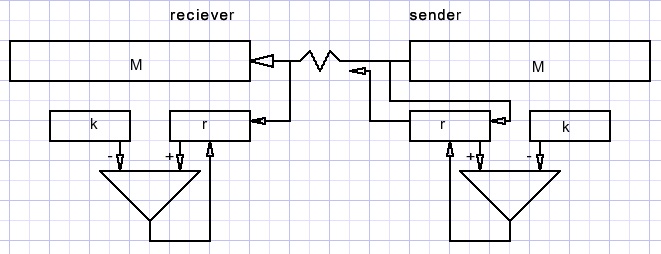
Aan de zenderzijde worden de bits van M ook in register r geschoven.
k wordt van r afgetrokken.
De rest r wordt direct achter M verzonden.
De ontvanger genereert eveneens r uit het ontvangen bericht.
Als M zonder fouten is verstuurd zal r gelijk zijn aan de ontvangen waarde r.

Beperkingen

In het geval van een bericht van 32 bits en een checksum (r) van 16 bits,
zijn er 2³²/2¹⁶ = 65536 berichten die dezelfde checksum opleveren.
Dat ziet er op het eerste gezicht dus slecht uit maar bedenk dan dit:
een willekeurige beschadiging van een bericht wordt alleen niet herkend
als er één van de 65536 mogelijke checksums is gegenereerd.
Met een checksum van lengte n is de kans op een ongeziene willekeurige fout 1 / 2ⁿ.

Decimale uitleg

Om CRC checking te begrijpen rekenen we even in het 10 tallig stelsel en nemen een sleutel 10.
Het bericht 192743 genereert dan een checksum 3 ongeacht de andere cijfers.
Elke fout in andere cijfers dan de 3 blijft onopgemerkt.
De reden is dat 40, 700, 2000, 90000, 100000 veelvouden van 10 (de sleutel) zijn.
Neem nu 11 als sleutel. 192743₁₀ = 1218a1₁₁ {a = 10}
Nu is de CRC code 1.

Een fout treedt op, M wordt 195743₁₀ = 124079₁₁ en de checksum is nu 9.
De fout wordt opgemerkt.

Neem eens een sleutel van 125.
8 * 125 = 1000 dus fouten in cijfer posities 3,4,…etc blijven onopgemerkt
omdat de fouten een veelvoud van 125 zijn.
Dit brengt ons tot een belangrijke conclusie:
een fout E in bericht M blijft onopgemerkt als E een veelvoud is van sleutel k.
Decimaal rekenend mag 10ⁿ geen veelvoud zijn van k voor n = 1,2,3,…..
Dit is het geval als er geen gemeenschappelijke factoren zijn.
Met een sleutel van k bits lang, wat checksums oplevert van n = k-1 bits,
wordt elke fout binnen het gebied van n bits gedetecteerd.

Openbaar of geheim?

In het geval van data transmissie is een openbare sleutel prima.
Maar dat is anders als CRC checking gebruikt wordt om de echtheid van een document te waarborgen.
In dat geval moet een geheime sleutel worden toegepast
die alleen by de applicatie of opsteller van het bericht bekend is.

Versimpeld rekenen

Hiervoor vermeldde ik dat de checksum via deling tot stand komt.
Deling omvat aftrekken en "lenen" (eng. borrow) van hogere cijfers.
Die borrows zijn te vermijden door de bewerking aftrekken te vervangen door de logische bewerking Exclusive Or.
Deze versimpeling gaat niet ten koste van de effectiviteit van CRC checking.

De binaire XOR bewerkingen zijn: 0+0 = 0; 0+1=1; 1+0=1; 1+1=0;
Geen "onthouden" (carries) of "lenen" (borrows), die worden simpelweg vergeten.
Er is nu geen verschil meer tussen optellen en aftrekken.
XOR heet ook wel "logisch verschil".

Ook bij XOR is de 0 het eenheidselement: 1+0 = 1, 0+1 = 1.
1 is zijn eigen omgekeerde: 1 + 1 = 0.
De associatieve wet geldt: (a+b) + c = a + (b+c)
De commutatieve wet geldt: a+b = b+a
De distributieve wet geldt: a(b+c) = ab + ac
zie het volgende voorbeeld waarbij a=1001, b=1100 en c=0111

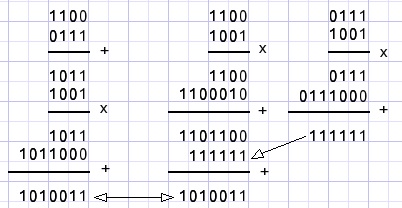
Links zien we a(b+c) en rechts ab + ac. Geen verschil.
We hebben dus een werkend rekenkundig systeem.

Ik geef nog een geruststellend voorbeeld:
de berekening a * b / b = a voor a=010111 en b=101101

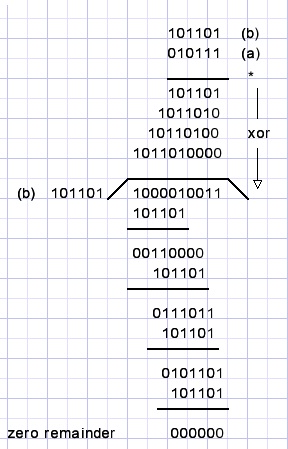
opmerking: in het quotient zijn we niet geïnteresseerd.

Sleutelkeuze

Een sleutel (key) van 1 0000 0000₂ zal checksums genereren die gelijk zijn aan de laagste 8 bits van M.
Reden is dat elke bericht xxx 0000 0000 een veelvoud is van de sleutel.
Elke andere key is OK.
De keuze van een bepaalde sleutel hangt af van het verwachte soort fouten.
Veel sleutels zijn ontworpen om fouten te zien in twee bits die verder van elkaar liggen.
In zo'n geval mag bijvoorbeeld 100000000000000001 geen veelvoud zijn van de sleutel.
De berekening moet natuurlijk worden uitgevoerd met de hiervoor genoemde xor bewerkingen.

Populaire sleutels

Een populaire 16 bits sleutel is 1 0001 0000 0010 0001 de X25 standard genoemd.
Een ander 16 bit key is 1 1000 0000 0000 0101 het CRC-16 protocol, gebruikt door modems.
De Ethernet standaard gebruikt de 32 bit key 1 0000 0100 1100 0001 0001 1101 1011 0111

Deze sluetels zijn ontworpen om dubbel bit fouten te detecteren de verder uit elkaar liggen.
De keuze van een bepaalde sleutel is afhankelijk van de verwachte fouten.

Praktijk

I heb een rekenmachientje geprogrammeerd voor binair rekenen.
Carries en borrows zijn te blokkeren wat rekenen met CRC codes mogelijk maakt.
Bewerkingen worden bit voor bit uitgevoerd.
De snelheid is daarbij instelbaar van 1 tot 25 bits per seconde.

Getallen zijn zowel binair, decimaal of hexadecimaal in te voeren.
De link naar dit programma staat bovenaan deze pagina.