De cirkel illusie

Het plaatje hieronder toont twee cirkels met middelpunten M en N.
De kleine cirkel raakt de grote inwendig in punt P en heeft de halve diameter.
De kleine cirkel rolt wrijvingsloos binnen de grote.
Het middelpunt N van de kleine cirkel beweegt aldus over de groene cirkel.
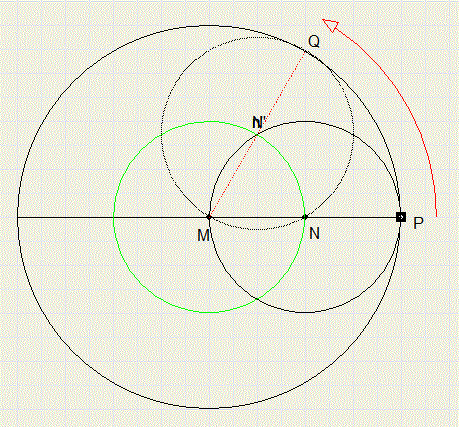
Na draaiing is middelpunt N aangekomen in N'.
Het nieuwe inwendige raakpunt is Q.
Vraag:
    welke weg legt punt P af, als die vastzit aan de kleine cirkel?
In het plaatje hierboven is lijnstuk MN gedraaid naar MN', laten we deze hoek v noemen.
Bij hoek v hoort een booglengte op de grote cirkel van vp/180, als de straal van de grote cirkel 1 is.

Omdat de kleine cirkel de halve straal heeft, zal de hoekverdraaiing het dubbele bedragen.
Ook is de draaiing met de klok mee.

De nieuwe positie van punt P na verdraaiing over v graden is dus de optelling van twee verdraaiingen:
    1. middelpunt N naar N', over v graden linksom
    2. punt P op de kleine cirkel, over 2v graden rechtsom
MP' = MN' + N'P'

Bekijk nu het plaatje hieronder
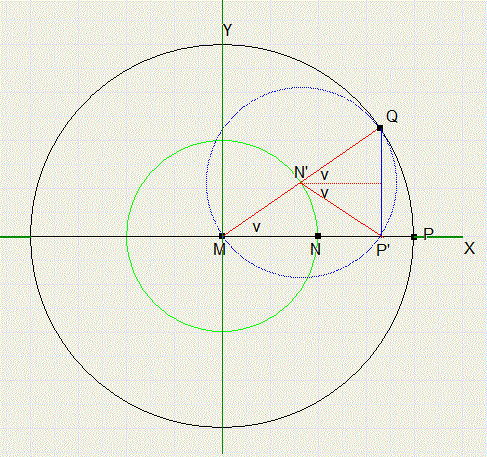
De positie op de X-as van punt P wordt dus : X = 0,5cos(v) + 0,5cos(-v) = cos(v)
De positie op de Y-as van punt P wordt dus : Y = 0,5sin(v) + 0,5sin(-v) = 0,5sin(v) - 0,5sin(v) = 0

Punt P beweegt dus over de middellijn van de grote cirkel.

Op het web staat dit leuke filmpje, genaamd "crazy-circle-illusion".
Hierboven staat de wiskundige verklaring.