

 |
Grafieken Verbouwen |  |
 |
Rekenregels, vergelijkingen en functies
Bekijk eens
| 3(2x - 5) = 6x - 15 |
Dit is een rekenregel: welke waarde voor x ook wordt ingevuld, links en rechts
van het = teken is de uitkomst steeds hetzelfde.
Bekijk nu
| 3(2x - 5) = 39 |
Er is nu maar 1 waarde van x waarvoor dit klopt, nl. x = 9.
Dit heet een vergelijking. x=9 is de oplossing van deze vergelijking.
Bekijk de vergelijking
| 2y - 5x = 10 |
Voor elke waarde van x, die we invullen, is een waarde van y te vinden,die
de vergelijking kloppend maakt.
Deze vergelijking heeft dus oneindig veel oplossingen. Elke oplossing is te
schrijven als een getallenpaar (x,y).
Zo zijn (0,5) en (-2,0) oplossingen, maar (8,8) is dat niet.
Als we in een coördinatenstelsel een punt zetten op alle oplossingen (x,y),
dan ontstaat een grafiek.
Bij grafieken zetten we het getal waarvan wordt uitgegaan horizontaal en
de berekende uitkomst vertikaal.
Vaak zal horizontaal de tijd staan of een afmeting en vertikaal bijvoorbeeld
de afgelegde afstand of een inhoud.
Weten we niet waar het over gaat, dan zetten we horizontaal x en vertikaal y
De vergelijking hierboven is te verbouwen tot:
| y = 2,5x + 5 |
Deze vorm is handiger: x invullen en y is simpel uit te rekenen.
Als een vergelijking zo is geschreven - de uitkomst alleen links - dan spreken
we van een functie. Een functie kan dus voor een waarde van x hoogstens
een waarde (van y) opleveren.
We onderzoeken nu hoe vergelijkingen en functies veranderen, als de grafiek wordt
verschoven, uitgerekt of gespiegeld.
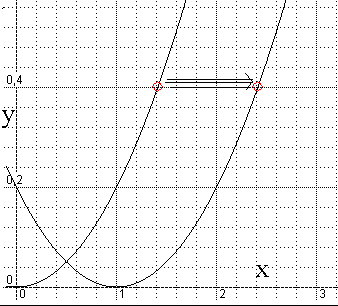
Horizontaal verschuiven
Rechts zie je de grafiek van y = 0,2x2,
en zijn horizontale verschuiving
met 1 naar rechts.
Beschouw een willekeurige vergelijking
...x...y...= ...x...y...
De stippeltjes zijn getallen en +,-,* en / tekens.
Neem eens aan, dat de vergelijking klopt voor x = 1 en y = 0.2, dus (1 , 0.2)
Nu vervangen we consequent in de vergelijking (x) door (x-1) zodat
...(x-1)...y...= ...(x-1)...y...
De vraag is, voor welke getallenparen (x,y) de vergelijking nu klopt.
Welnu, dat zal het geval zijn als (x,y) in de eerste vergelijking gelijk is
aan (x-1,y) in de nieuwe. Dus in plaats van x = 1, nu voor (x-1) = 1 of x = 2.
Het punt (1, 0.2) is verschoven naar (2, 0.2)
Het effect van (x) vervangen door (x-1) is dus een verschuiving van de grafiek
over afstand 1 naar rechts.
In plaats van (x) te vervangen door (x-1) hadden we ook (x+1),(y-1),(x/2) of
wat dan ook kunnen nemen. Met bovenstaande redenatie is steeds na te gaan wat het
effect op de grafiek zal zijn.
De mogelijkheden op een rij
| vervangen door | dan zal de grafiek | |
| x | x-1 | 1 naar rechts schuiven |
| x | x+1 | 1 naar links schuiven |
| y | y-1 | 1 naar boven schuiven |
| y | y+1 | 1 naar beneden schuiven |
| x | x/2 | een factor 2 t.o.v. de y-as uitrekken |
| y | y/2 | een factor 2 t.o.v. de x-as uitrekken |
| x | -x | spiegelen om de y-as |
| y | -y | spiegelen om de x-as |
| x y | -x -y | spiegelen om (0,0) |
Zelf oefenen
Start het programma "GraphicsExplorer"of download het eerst.
Tik in: y = 0,5(x-a) - 3
Selecteer "vervangen" en "autoplot". Druk muisknop in boven A-venster
zodat A van waarde verandert. Bekijk het effect op de grafiek.
Als y wordt vervangen door (y-b) dan (y-b) = 0,5(x-a)-3 of
y = 0,5(x-a) - 3 + b
Tik ook deze functie in en bekijk hoe de grafiek verandert met A en B.
Onderzoek zelf andere formules, bijvoorbeeld y = x/a + b , y = a*sin(x/b + c)
of 2(x-a)2 + (y-b)2 = 64
Voorbeeld 1
De functie y = 2x - 5 wordt 5 naar links geschoven:
Schrijf eerst y = 2(x) - 5 , vervang nu x door x+5 en de nieuwe functie wordt
y = 2(x+5) - 5
y = 2x + 5.
Voorbeeld 2
De functie y = x2-5x + 1 wordt 4 naar rechts en daarna 7 omlaag geschoven:
Schrijf eerst y = (x)2-5(x) + 1
vervang x door x-4 en y door y+7 zodat:
y+7 = (x-4)2-5(x-4) + 1 of y = x2-13x + 30 is het resultaat.
Voorbeeld 3
We spiegelen de functie y = 3x-7 om het punt(2,9).
Daarvoor is geen recept bekend, er moet in stappen worden gewerkt:1. verschuif het assenstelsel zo, dat het punt(2,9) op (0,0) komt te liggen.
2. spiegel de grafiek om (0,0)
3. schuif het assenstelsel terug naar (2,9)
[1] in y = 3(x) - 7 vervangen we y door y+9 en x door x+2 zodat
y+9 = 3(x+2) - 7 of y = 3x - 10
[2] vervang in y = 3x - 10 (y) door (-y) en (x) door (-x) zodat -y = 3(-x) - 10
of y = 3x + 10
[3] vervang hierin y door y-9 en x door x-2, y-9 = 3(x-2) + 10 en
y = 3x + 13 is het antwoord.
Voorbeeld 4
x2 + y2 = 25 is de vergelijking van een cirkel met middelpunt (0,0) en straal 5.
Een cirkel van dezelfde grootte met middelpunt (3,7) heeft als vergelijking:
(x-3)2 + (y-7)2 = 25.
Toepassing
We zoeken een formule, die op tijd t de hoogte van een gondeltje in een
reuzenrad aangeeft, als dit ronddraait.
De omwentelingstijd is T seconden, de straal is R en de bezoeker start
op het laagste punt, dat 1 meter boven de grond ligt.
Om de gedachten te bepalen gaan we eerst uit van een dwergenrad.
Dat heeft een straal van 1, het middelpunt ligt op de grond, zodat
het rad half in de grond draait, de omwentelingstijd is 1 seconde en
de dwergen stappen rechts in. Het rad draait tegen de klok.
Hoogte h is nu h = sin(a) bij draaihoek a (in graden).
a is zelf weer een functie van de tijd t volgens a = 360t.
Combinerend: h = sin(360t)
Nu is de straal niet 1 maar R, zodat de hoogte h een factor R moet worden uitgerekt.
Dat kan door h door h/R te vervangen.
h/R = sin(360t) of h = R*sin(360t).
Als de bezoekers 1 meter boven de grond instappen, dan bevindt het middelpunt
van het rad zich op R+1 meter hoogte. Vervang dus h door h-(R+1) en
h = R*sin(360t) + R+1 beschrijft de beweging van een rad van de juiste afmetingen.
Deelname aan de attractie moet echter nog worden ontraden: de omwentelingstijd
bedraagt slechts 1 seconde. Een dodelijke attractie.
De periode moet van 1 naar T seconden worden opgerekt. Dat doen we door t te vervangen
door t/T.
h = R*sin(360*t/T) + R+1 is al een realistischer formule. Alleen stappen
de bezoekers nog R+1 meter boven de grond in. Het instappunt (moment) moet
T/4 worden vervroegd, wat we doen door t te vervangen door t-T/4.
De grafiek van de hoogte moet immers T/4 naar rechts schuiven.
(Ook kan worden uitgegaan van h = sin(a), a te vervangen door a-90)
Resultaat: h = R*sin(360t/T - 90) + R+1 geeft hoogte h van een gondeltje
in het reuzenrad met omwentelingstijd T, straal R op t seconden na de start
op het onderste punt, dat zich op 1 meter boven de grond bevindt.
Symmetrie
Een grafiek heeft een bepaalde symmetrie als er ondanks een ingreep geenverandering optreedt.
Zo is de grafiek van de cirkel x2 + y2 = 100 symmetrisch
om de x-as: y vervangen door -y verandert niets aan de vergelijking.
De grafiek van y = x3 is symmetrisch t.o.v. (0,0) want als we
zowel x door -x als y door -y vervangen, dan is er geen verschil te zien.
Als in een vergelijking zowel x als y alleen met oneven machten voorkomen,
dan zal de grafiek symmetrisch om (0,0) zijn.
Opgaven/suggesties
1. Ga uit van y = 2x - 5 en ga na hoe de functie verandert als de grafiek:
a. 4 naar rechts wordt verschoven
b. 2 naar links en 5 omlaag wordt verschoven
c. een factor 3 t.o.v. de y-as wordt uitgerekt
d. een factor 1/2 t.o.v. de x-as wordt uitgerekt
e. om de x-as wordt gespiegeld en daarna 1 omlaag wordt geschoven
2. Ga uit van y = x2 en bepaal de nieuwe functie als de grafiek
a. 3 naar links schuift
b. 4 omhoog schuift
c. wordt gespiegeld om (10,0)
3. Leg uit, dat spiegelen om (0,0) kan worden bereikt door spiegelen om
de x- en daarna om de y-as.
4. Welke ingreep moet je toepassen op een vergelijking om de grafiek te
spiegelen om de lijn y = x?
5. Welke betekenis heeft spiegelen in y = x voor een functie?
6. De functie y = 1,5x - 9 wordt 6 naar rechts en daarna 9 omhoog geschoven.
Hoe verklaar je dit resultaat?
7. Ga in de volgende gevallen na of de volgorde van belang is als een functie:
a. naar rechts wordt geschoven en daarna wordt gespiegeld om de x-as.
b. naar rechts en omhoog wordt geschoven en daarna gespiegeld om de y-as.
c. eerst wordt gespiegeld in (0,0) en daarna om de y-as.
8. Waar of onwaar:
Een functie spiegelen om de lijn y = ax kan je bereiken door eerst het
coðrdinatenstelsel uit te rekken met een factor a in de x-richting,
dan te spiegelen om y=x en vervolgens het coðrdinatenstelsel in de x-richting
te rekken met een factor 1/a.
9. Welke symmetriën kan je in de volgende vergelijkingen zien?
a. 2x2 + y2 = 49
b. y = 5x
c. xy = 5
d. (x - 4)(y - 4) = xy
e. (x2 - 10)(y2 + 2) = 2xy4
f. y = x3 + 3x
g. y = 3x4 - 5x2 + 10
10. x wordt vervangen door 2a-x. Wat is het effect op de grafiek?


