

| Booleaanse Algebra |  |
Inleiding
Booleaanse algebra is een soort algebra, die wordt gebruikt bij het ontwerpen van computersen andere digitale apparatuur.
Ook is er toepassing in computerprogramma's zoals zoekmachines en in het algemeen in de logica.
Booleaanse algebra is een rekenkundige invulling van de propositielogica.
Ook zijn er sterke overeenkomsten met de verzamelingentheorie.
De Booleaanse algebra is bedacht door de Britse wiskundige George Boole (1815 - 1864).
Klik [ HIER ] voor Logic10 , een programma dat formules met Booleaanse Algebra verwerkt.
Variabelen en operatoren.
Een Booleaanse variable kan de waarden "true" of "false" aannemen.Voor een rekenkundige aanpak heeft "true" de waarde "1" en "false" de waarde "0".
In dit artikel wordt een Booleaanse variabele aangegeven met een enkele letter, zoals A of B.
De variable staat dan voor een bewering of een bepaalde toestand zoals: "start switch ingedrukt" ,
"temperatuur OK", "het is 10 uur" , "John is ziek" ....etc.
De bewering of toestand (propositie) is waar of onwaar.
De zon schijnt, of niet. Een schakelaar is open of dicht.
Eén variable is de kleinst mogelijke hoeveelheid informatie.
Informatie is in het algemeen de verkleining van onzekerheid.
In een vreemde stad op een kruising de weg vragend ("moet ik linksaf naar het station") is het kortste
antwoord ja of nee. (0 of 1).
In het Engels heet een cijfer "digit". Tweetallig is "binairy".
De kleinste hoeveelheid informatie is één cijfer in het tweetallig stelsel.
Die noemen we bit, afkorting van Binairy Digit.
Hoe een bit informatie wordt gecodeerd hangt van de techniek af.
Een schakelaar kan ingedrukt "1" (true) weergeven.
Bij elektronica is bijvoorbeeld "1" en spanning hoger dan 2,2 volt en "0" een spanning onder de 0,8 volt.
Of een bepaalde stroom geldt als "1" , geen stroom als "0".
Bewerkingen
Om twee variabelen of meer te combineren tot een meer complexe bewering of situatie,zijn er twee bewerkingen: AND en OR
Ook is er een bewerking not, die de bewering omdraait.
not 0 = 1 en not 1 = 0
not is een unaire operator: die bewerkt één variable inplaats van twee.
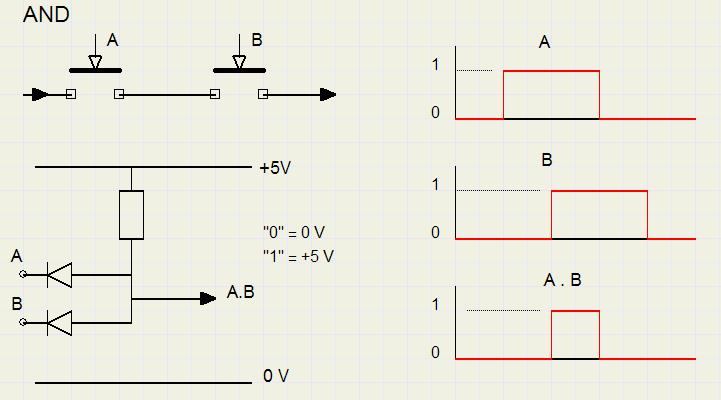
AND
De operator voor AND is "." (punt)| A | B | A.B |
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
In een AND gezin moeten beide ouders accoord gaan als een kind iets vraagt.
AND heet ook wel : "logisch product".
In de elektromechanica wordt een AND functie toegepast door schakelaars in serie te zetten.
Er kan alleen stroom lopen als beide schakelaars zijn ingedrukt.
In de elektronica heet een circuit dat een AND functie vervult een AND gate.
Voor de AND bewerking gelden de associatieve- en de commutatieve wetten:
A.(B.C) = (A.B).C
A.B = B.A
Hieronder staan uitvoeringen van AND gates, elektronisch met diodes en met schakelaars.
Afspraak is, dat een ingedrukte schakelaar de "1" toestand is.
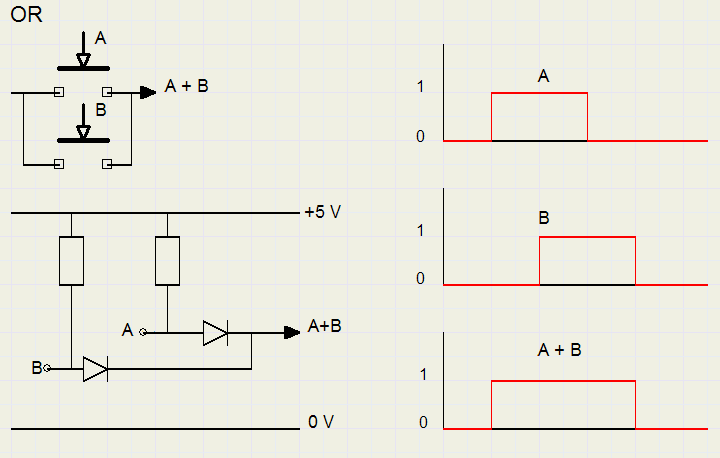
OR
De operator voor OR is "+"| A | B | A+B |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
In een OR gezin volstaat toestemming van één van de ouders.
Voor OR bewerkingen gelden de associatieve- en de commutatieve wetten:
A+(B+C) = (A+B)+C
A+B = B + A
OR heet ook wel "logische som".
In de elektromechanica wordt een OR gerealiseerd door schakelaars parallel te plaatsen,
stroom loopt als één van de schakelaars aan staat.
In de elektronica heet een schakeling die een OR functie vervult een OR gate.
Hieronder staat afgebeeld een OR met schakelaars en elektronisch, met diodes.
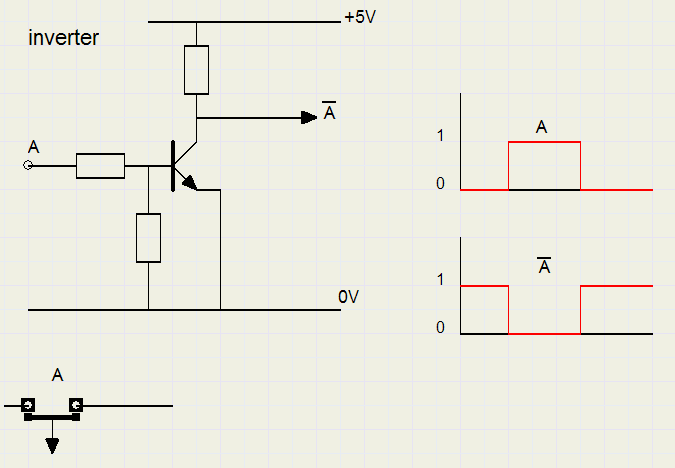
NOT
Not is de omkering van een waarde.NOT is een unaire operator, die voor een variabele wordt geplaatst.
In de Booleaanse algebra wordt not gewoonlijk aangegeven met een horizontaal streepje boven de variabele,
zoals
Omdat zo'n streepje lastig is met editen van tekst, gebruikt dit artikel een /.
Dus: not A = /A =
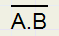
| A | NOT A |
| 0 | 1 |
| 1 | 0 |
Stel eens dat A = "schakelaar ingedrukt" en B = "stroom loopt",
dan is B = /A als de schakelaar bij indrukken de stroom verbreekt.
In de elektronica heet een circuit, dat de not functie vervult, een inverter.
Hieronder staan mogelijke inverters afgebeeld.
De schakelaar verbreekt de stroom bij indrukken.
De transistor is stroomversterker versterker en draait tevens de spanning om.
In de praktijk worden de AND - en OR gates met diodes altijd gevolg door een inverter
omdat anders het signaal verzwakt.
And gates, Or gates en Inverters zijn de (enige) bouwstenen van computers.
Hiermee worden complexere functies gemaakt zoals optellers, decoders, multiplexers, timing chains en geheugens.
XOR
Een voorbeeld van een complexere bouwsteen is de XOR gate(exclusive OR, ook wel: logisch verschil of halve opteller).
De formule luidt: A xor B = A./B + /A.B.
XOR is de bouwsteen voor telwerken en optellers.
Een XOR tussen A en B levert "1" op als A en B ongelijke waarden hebben.
Merk op: ook voor xor geldt de commutatieve en de associatieve wet.
Extra is, dat de xor functie zijn eigen inverse is, want A XOR B XOR B = A
Hieronder staan de symbolen voor AND- OR gates en inverter.
Ook is een XOR schakeling weergegeven.
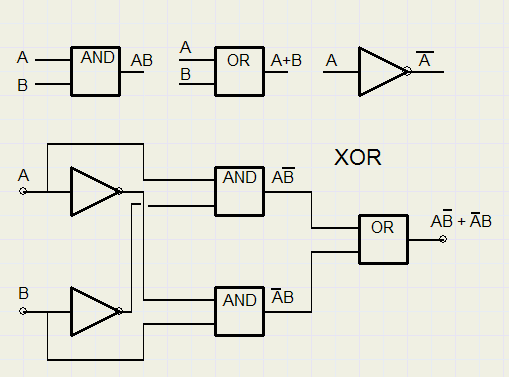
Meerdere variabelen
AND , OR bewerkingen kunnen meer variabelen omvatten dan twee.De formule A.B.C.D levert alleen een "1'" als A,B,C,D allemaal de waarde "1" hebben.
De formule A+B+C+D levert een "1" als minimaal één van de variabelen A,B,C,D de waarde "1" heeft.
De formule A./B.C levert een "1" als A=1, B=0 (dus /B=1) en C=1.
Distributieve wetten
Boolean algebra kent twee distributieve wetten met de AND en OR operators.-
1..........A.(B+C) = A.B + A.C
2..........A + B.C = (A+B).(A+C)
Laat namelijk de variabelen alle mogelijke waarden doorlopen en controleer op gelijke uitkomsten.
Voor distributieve wet 1. wordt dat
| A | B | C | A(B+C) | AB+AC |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 |
Het bewijs van distributieve wet 2. wordt aan de lezer overgelaten.
Inconsistent
Een formule heet inconsistent als het resultaat nooit "1" wordt, ongeachte de waarden van de variabelen.Een eenvoudige inconsistentie is : A./A
Tautologie
Een formule is een tautologie als de waarde altijd "1" is, ongeachte de waarde van de variabelen..Een eenvoudige tautologie is A + /A
Regels voor vereenvoudiging van formules
Een complexe formule kan soms worden vereenvoudigd.De redundantie wordt eruitgeperst, wat onderdelen bespaart of een programma versimpelt.
Vereenvoudigingsregels zijn:
-
1...A + A = A
2...A + A.B = A
3...A . B + A . /B = A
4...A + /A . B = A + B
-
A./A = 0
A + /A = 1
1. Volgt uit de definitie.
2. Distributieve wet: A + A.B = A.(1 + B) = A
3. Distributieve wet: A./B + A.B = A.(/B + B) = A
4. Distributieve wet 2: A + /AB = (A + /A)(A + B) = 1.(A + B) = A + B
Het bewijs van een regel voor vereenvoudiging is opnieuw te leveren door de variabelen alle waarden
te laten doorlopen en de resultaten te vergelijken.
| A | B | C | A.A | A+A | A+B | A.B+A./B | A+/A.B |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
De Morgan's wetten
|
1....../A + /B = /(A.B) 2....../A . /B = /(A +B) |
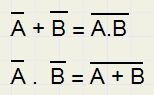 |
Het bewijs is voor de lezer.(vergelijk uitkomsten voor alle waarden van A,B)
De Morgan's wetten zeggen dat : een AND voor énen een OR is voor nullen en ook :
een OR voor énen is een AND voor nullen.
Als een motor wordt aangezet door twee schakelaars in serie,
dan volstaat het één schakelaar uit te zetten om de motor te stoppen.
Een bewijs van regel 4 met de wetten van De Morgan:
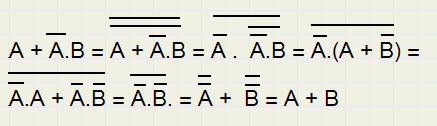

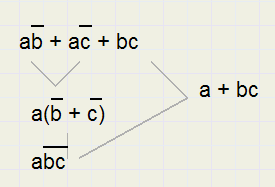
In de onderstaande formule is de term ac overbodig.
Dat is in te zien door splitsing: ac = abc + a/bc, daarna termen combineren:
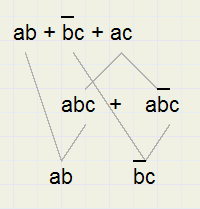
Waarheidstabellen
Een waarheidstabel is een lijst van waarden van variabelen, die een formule "waar" maken, dus "1" opleveren.Een waarheidstabel heeft de vorm: A.B.C + D.E.F + G.H.I + ........
De AND bewerkingen staan per regel, regels worden geORed.
Deze vorm heet ook wel de "conjunctieve normaalvorm".(CNF)
Voorbeeld
In digitale apparatuur worden vaak 7-segment displays gebruikt om een cijfer weer te geven.Per cijfer zijn 4 bits nodig, laten we die noemen A(bit-0-) , B(bit-1-) , C(bit-2-), D(bit-3).
We bouwen een waarheidstabel voor de gevallen waarin het bovenste segment aan moet zijn.

| digit | A | B | C | D |
| 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 |
| 6 | 0 | 1 | 1 | 0 |
| 7 | 1 | 1 | 1 | 0 |
| 8 | 0 | 0 | 0 | 1 |
| 9 | 1 | 0 | 0 | 1 |
a "0" betekent dat de variabele "0'" moet zijn (/A,/B,/C.....)
De eerste 3 regels van de tabel betekenen: /A./B./C./D + /A.B./C./D + A.B./C./D
De tabel kan worden vereenvoudigd met de regel A./B + A.B = A.(/B + B) = A
Voor A lezen we de gelijke variabelen, B en /B geven een verschil van 1 bit aan (0 vs 1, of 1 vs 0).
In regels 1 en 2 verschilt alleen bit 1 van waarde, zodat die regels gecombineerd kunnen worden to 0x00,
waarbij x (hier B) er niet toe doet.
Ook bij cijfers 5,7 is bit B het enige verschil, dus kunnen deze regels worden vervangen door 1x10.
Regels voor cijfers 8,9 worden net zo gecombineerd tot x001.
De tabel is nu verkort tot:
| A | B | C | D |
| 0 | x | 0 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | x | 1 | 0 |
| 0 | 1 | 1 | 0 |
| x | 0 | 0 | 1 |
Regels 2,4 nu bekijkend kan bit C in regel 4 verwijderd worden.
De uiteindelijke waarheidstabel wordt:
| A | B | C | D |
| 0 | x | 0 | 0 |
| x | 1 | 0 | 0 |
| 1 | x | 1 | 0 |
| 0 | 1 | x | 0 |
| x | 0 | 0 | 1 |
dat het bovenste segment uit is, Daarna een omkering toepassen.
Toepassingen
Elektro mechanica
Dat houdt in schakelaars en relais: gebruikt in procesautomatisering om bv motoren aan te sturen.Schakelaars bestaan in vele soorten en maten: maak, verbreek, momenteel, toggle, voor grote en kleine stroomsterkten......
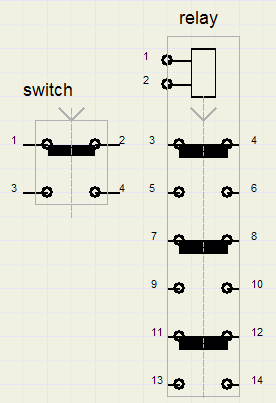
Een relais is een schakelaar die magnetisch wordt aangestuurd: stroom door een spoel maakt ijzer magnetisch.
Hierdoor wordt een ijzeren kern of plaatje aangetrokken en deze kracht bedient één of meer schakelaars.
Valt de stroom door de spoel weg, dan zorgt veerdruk voor terugschakelen.
Laten we de schakelaar A noemen en A = 1 betekent : A is ingedrukt.
Voor kontakten 1,2 is de functie dan /A omdat het zg. rustcontacten zijn: gesloten zolang de schakelaar
niet is ingedrukt. Kontakten 3,4 vervullen de functie A, omdat deze kontakten stroom geleiden als de schakelaar is ingedrukt.
Bij het relais zullen kontakten 5-6 ,9-10 en 13-14 stroom geleiden als er stroom door de spoel wordt gestuurd.
Zonder stroom door de spoel geleiden kontakten 3-4 , 7-8 en 9-10.
Omdat het relais alle benodigde functies kan vervullen kan er een complete computer mee worden gebouwd.
Bus Stop
Autobussen voor stad- en streekvervoer hebben stopknopjes boven de zitplaatsen.Die knopjes zijn momentele schakelaars, ze veren terug bij loslaten.
Toch is het niet nodig om het knopje tot de halte ingedrukt te houden.
Dat komt omdat er een (1 bit) geheugen wordt gebruikt om het stopverzoek te bewaren.
Stopt de bus bij de halte, dan moet het lampje uitgaan. De conditie "deuren open" is daar geschikt voor.
Hoe ziet zo'n schakeling eruit?
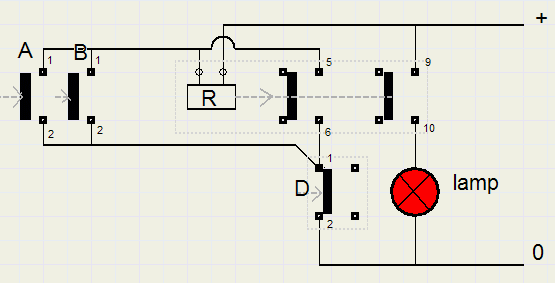
R is een relais. D is de deurschakelaar. D betekent : "deuren zijn open"..
Schakelaars en relais staan afgebeeld in ruststand.
Als een passagier op zijn stopknopje drukt, dan gaat stroom door de spoel en het relais trekt aan,
als de deuren gesloten zijn.
Kontakten 9,10 sluiten en het stoplampje gaat branden.
Laat de passagier het stopknopje los, dan blijft stroom lopen via contacten 5,6 zolang de deuren gesloten zijn.
De formule is: R = (A + B)./D + R./D = (A+B+R)./D
R zowel links als rechts van het = teken geeft de geheugenfunctie aan.
Elektronica
In computers worden logische functies gemaakt met elektronica omdat elektronische schakelaars (transistoren) het snelst zijn.Er zijn allerlei soorten logische circuits: DTL (diode transistor logic), TTL (transistor transistor logic),
RTL (resistor transistor logic) en de allersnelste is ECL (emitter coupled logic).
Ze hebben allemaal hun specifieke spanningsniveaus om een "0" of een "1" weer te geven.
Voor TTL bijvoorbeeld is een "0" 0 ....0.8 Volt en een "1" een spanning boven de 2.2Volt (voedingsspanning is 5 Volt).
In de praktijk wordt een AND- of OR gate altijd gevolgd door een inverter.
De combinatie van AND en inverter heet NAND gate.
De combinatie van OR en inverter heet NOR gate.
Als een gate voor de functie (AND,OR) een "0" levert dan wordt dat aangegeven met een rondje.
Hieronder staan een NAND en een NOR gate met een schema voor DTL logica.
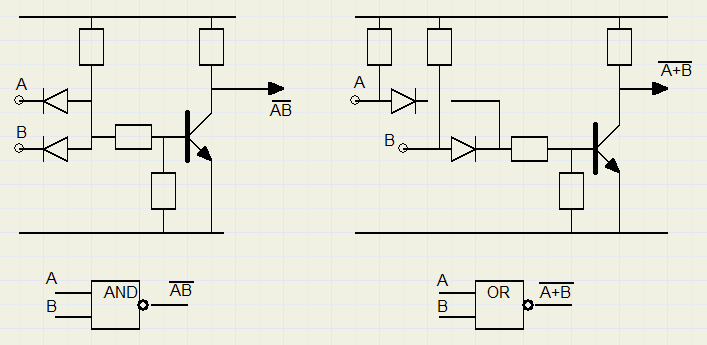
computer kan worden gebouwd met alleen NAND-gates.
In werkelijheid echter worden 2,3,4,8 input AND,NAND,OR, NOR gates en ook inverters toegepast.
Complexere functies
Hiervoor werd al genoemd de XOR gate, de bouwsteen voor optellers.Andere meer complexe functies zijn
-
- optellers..........(tellen 2 getallen op)
- multiplexers....(voegen signalen samen)
- decoders........(leveren "1" als een bepaalde conditie zich voordoet
- encoders........(genereren een code voor een bepaalde conditie)
- flip-flops..........( 1 bit geheugen)
- registers.........(een verzameling flip-flops die een getal bevatten)
- tellers.............(register dat kan verhogen/verlagen)
- shifters..........(verschuiven bits, bv bij parallel - serie omzetting)
- timing chains....(simpel soort telwerk voor procescontrole)
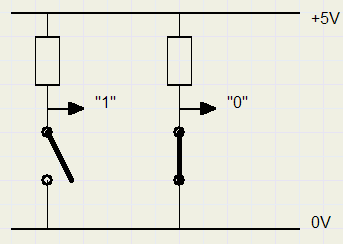
Nullen en Enen instellen
Stel dat in een bepaalde logica een "1" wordt aangegeven met een spanning > 3V en een "0" met 0V.Met een schakelaar is dan zo een "0" of "1" in te stellen, zie figuur hieronder:
Realistische signalen
Hiervoor tekenden we elektrische signalen die zonder tijdverlies tussen "0" en "1" omschakelen.Dat is niet realistisch, een AND gate, OR gate of inverter heeft een bepaalde schakeltijd.
De figuur hieronder laat een realistische puls zien:
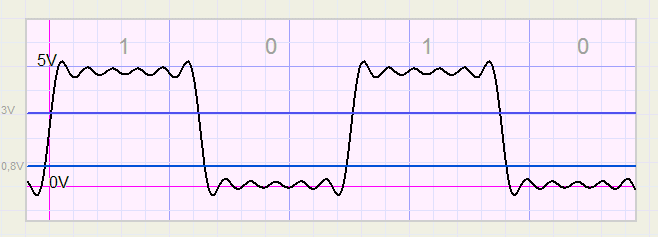
Tussen de 0,8 ... 3V is de waarde onbepaald.
Dit traject moet dus snel worden doorlopen.
Andere regel voor vereenvoudiging
Hiervoor pasten we vereenvoudigingsregels 1..4 toe.Met een nieuwe regel kunnen oude regels 3 en 4 vervallen terwijl andere vereenvoudigingen makkelijker
zijn in te zien.
Deze methode heb ik eind 2013 bedacht en in mijn programma logic10 met succes toegepast.
De regel luidt
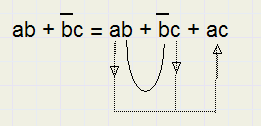
De overige factoren a en c (naast b, /b), mogen nu als term worden toegevoegd.
ab en /bc noem ik de parents van ac.
Term ac is overbodig, maar kan wel worden ingezet om de formule te vereenvoudigen.
Die vereenvoudiging mag niet inhouden dat de parents worden verwijderd, want die zijn juist de oorzaak van ac.
ac noem ik een virtuele term.
Hieronder geef ik vereenvoudigingsregels 1 en 2 nog eens:
-
1..... A + A = A
2.....A + AB = A
Daarna geldt AB + A = A
Regel4 : A + /AB levert de virtuele term B
daarna geldt: B + /AB = B
Virtuele termen aan het werk
Hieronder zijn de virtuele termen dikgedrukt.1.
-
/AP + /BP + /CP + ABC = ......
/AP + ABC ---> PBC
PBC + /BP ---> PC.................nieuwe virtuele term
PC + /CP ---> P
P + /AP = P etc.
zodat
/AP + /BP + /CP + ABC = P + ABC
-
ABP + CD/P + ABCDEF = .....
ABP + CD/P ---> ABCD
ABCD + ABCDEF = ABCD
zodat:
ABP + CD/P + ABCDEF = ABP + CD/P
-
ABP + A/C + BC = ...
A/C + BC ---> AB
AB + ABP = AB
zodat:
ABP + A/C + BC = AB + A/C + BC

