Boomstructuren programmeren
bekijk Delphi source listing van de Tree unit.
download Tree - exerciser program.
download complete Delphi - 7 project

Inleiding

In de wiskunde verstaan we onder een graaf een tekening met punten.
Elk punt hierin kan wel of niet met de andere punten zijn verbonden.
Grafentheorie gaat over de eigenschappen van grafen.
Grafen worden toegepast in bijvoorbeeld
    - landkaarten en plattegronden
    - elektrische netwerken
    - moleculen
    - industriële planning
    - informatietechnologie:
      - file systemen
      - computerspelletjes
      - tekstverwerking

Een graaf is een abstracte voorstelling om een samenhang van objecten of gebeurtenissen af te beelden.
Een (knoop) punt is daarbij de situatie of het object.
Zo'n knooppunt zal dus bepaalde eigenschappen hebben.
Een lijn tussen twee punten betekent dat er een overgang van de ene naar de ander situatie bestaat,
of dat het ene object op één of andere manier van het andere afhankelijk is.
Hieronder staat een zg. volledige graaf, elk punt is eenmaal met elk ander punt verbonden.

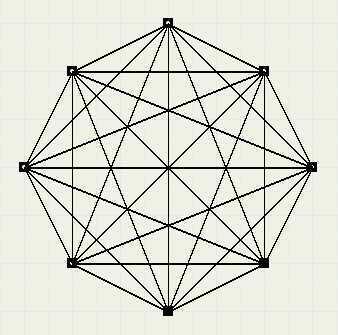
Als in bovenstaande graaf een punt een persoon voorstelt, dan kan een lijn bijvoorbeeld aangeven
dat er handen worden geschud.
In een volledige graaf zijn er bij n punten n(n-1)/2 lijnen.
Als de graaf een computernetwerk is, dan is elke lijn een rechtstreekse dataverbinding.
Om 20 computers direct met elkaar te verbinden zijn dus 20(19)/2 = 190 kabels nodig.
Als op een feest 20 mensen elkaar de hand schudden, dan moeten er 190 paar handen worden geschud.


Bomen (Engels: Tree)

Een boom is een bepaald type graaf.
Als bij een boom een lijn wordt weggehaald, dan ontstaat een afgesplitste boom:
vanuit de ene tak zijn punten van de andere tak niet meer te bereiken.
Een andere eigenschap van een boom is, dat de route van punt A naar B langs dezelfde punten
verloopt als de route van B naar A. Er zijn geen rondwegen.

Hieronder staat een voorbeeld van een boom, bekend misschien van de kansrekening.

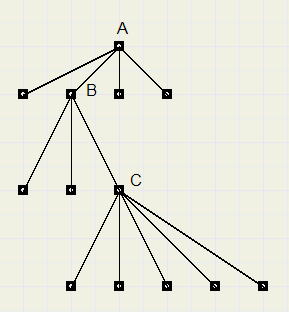
Deze graaf zou een filesysteem kunnen voorstellen met een map A die vier bestanden bevat,
waaronder map B, die weer drie bestanden bevat waaronder map C, met daarin vijf bestanden.

Dit artikel gaat over het programmeren van boomstructuren.
Dat houdt in het creëren van bomen, het aanbrengen van veranderingen en ook het weer ongedaan maken
van die veranderingen (undo).
Het Delphi project bestaat uit twee units
    1. de tree_unit met de datastructuren, procedures en functies voor de boom
    2. unit1, met een form met knoppen om bewerkingen in 1. uit te voeren en te bekijken.
Het doel is om bewerkingen op bomen te testen voor toepassing in een wiskundige tekst editor.
Dat is een editor, die ook wortels, breuken, matrices, indices, machten etc. aan kan.
De punten in de graaf stellen dan de elementen voor (regels, letters, cijfers, operatoren, breuken,wortels, matrices...)

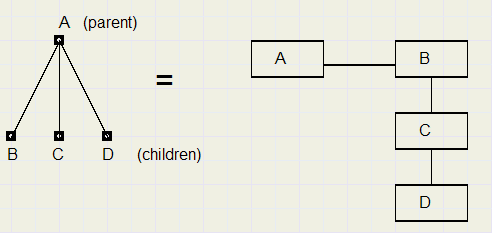
Hierboven staat een (tree) graaf met elementen A,B,C,D.
A is de ouder (parent) en B,C,D zijn de afstammelingen (children).
A kan een tekstregel zijn met daarin de letters B, C en D.
Links staat de wiskundige notatie, rechts staat de ICT notatie zoals we die kennen van het filesysteem
(mappen en bestanden).
Een element is een record met een aantal velden.
De elementen staan in een array[1.. ] zodat elk element meteen een nummer heeft 1,2,3,......(0 is geen element).
Hoe geven we nu aan welke lijnen er tussen de elementen lopen?
Dat gebeurt met de velden parent , child , next en previous.
type Telement = record
                 parent   : dword;
		    child    : dword;
		    next     : dword;
		    previous : dword;
                .................;//properties , codes, x, y, width, height.....
		   end; 
		   
var element : array[1..500000] of Telement;

Opmerking: dword = cardinal. Het aantal elementen is ca. 500.000, net zoveel als letters in een roman.


Als van element[8] het veld parent de waarde 2 heeft, dan is element[2] de parent van element[8].
Elk element heeft één veld om een child aan te geven.
Maar een element kan veel meer dan één child hebben.
Dit probleem wordt ondervangen met het veld next.
In de figuur hierna zijn elementen 2,3,4 children van element[1]

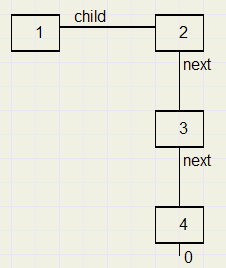
Let op: de elementen 2,3,4 hebben alle element[1] als parent.
Hier wordt dus dezelfde situatie uitgebeeld als hiervoor met elementen A,B,C,D.

Bij het veranderen van de bomen is het handig om van elk element ook direct te kunnen zien
wat het vorige (child) is.
Daarvoor is het veld previous.
In de graaf hierboven zijn elementen 2 en 3 opvolgende children van element[1], zodat 
    element[2].next = 3
    element[3].previous = 2
Hierna geef ik een element zo aan (een ontbrekend pootje geeft waarde 0 aan)

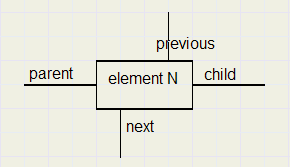
Als dus element[10] als kinderen elementen 20,21,22 heeft dan is
    element[10].child = 20...............{eerste kind}
    element[20].next = 21................{tweede kind}
    element[21.next = 22.................{laatste kind}
    element[20].previous = 0
    element[22].next = 0
    element[20].parent = 10
    element[21].parent = 10
    element[22].parent = 10

Toepassing in een wiskunde editor

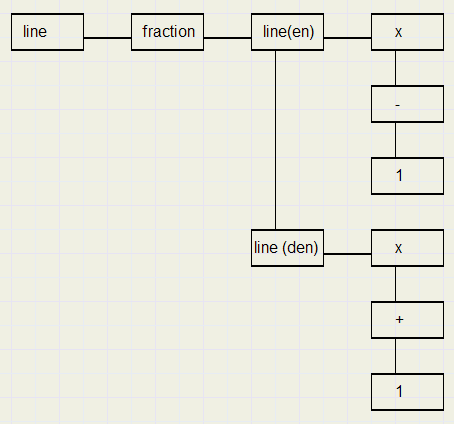
Hieronder staat een breuk (fraction), met teller en noemer, uit een stukje wiskundige tekst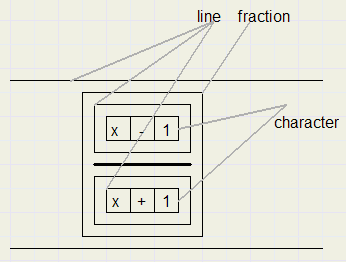

Een tekstregel (line element) bevat als child een breuk (fraction element).
Een fraction element heeft 2 lines als children, de teller (enumerator) en de noemer (denominator).
De teller (line) heeft als children de elementen met code x, - , 1
de noemer line heeft als children de elementen x, +, 1.

Dit is de opzet: elk element
    - is van een bepaald type (line, character, fraction.......)
    - heeft ook velden x,y , width, height..... voor vastlegging van de positie t.o.v. zijn parent
    - heeft velden die eigenschappen aangeven (code, kleur, stijl....)
Elk element heeft genoeg informatie om zichzelf te kunnen tekenen.
Een parent bepaalt de positie van de children.
Die positie (x,y) is altijd relatief t.o.v. de parent.
Stel, dat in de breuk hiervoor de teller verandert van x - 1 naar 1 en de noemer naar 2x + 25.
Een element rapporteert een verandering aan zijn parent, zodat de positie van die elementen opnieuw
berekend kan worden.
Ook moet de parent opnieuw de eigen afmetingen berekenen en een wijziging aan de eigen parent doorgeven.
In dit geval zal de noemer groter worden, wat een langere breukstreep inhoudt
en de positie van de teller zal netjes in het midden worden uitgelijnd.

Samengevat
    - de bewerkingen op de boomstructuur zijn voor alle elementen gelijk (maar het effect is dat niet)
    - per type element moet er een aparte procedure zijn voor
      - het creëren van het type element
      - het tekenen van het element
      - het berekenen van de eigen afmetingen
      - het berekenen van de posities van eventuele children
De breuk hierboven levert deze graaf op

Bewerkingen

De volgende bewerkingen op een boomstructuur komen aan de orde
    insert aftervoeg element in na een ander element
    insert beforevoeg element in voor een ander element
    insert childvoeg een child toe aan een kinderloos element
    deleteverberg een element
    replacevervang een element door een ander, verberg het oude element
    packplaats een element binnen het vorige element
    undomaakt vorige bewerking ongedaan

Insert after

Deze bewerking voorziet in het invoegen van tekens in een tekstregel,
maar ook in het invoegen van regels op een pagina.
Na element A wordt E ingevoegd.
Stel, dat element A als nummer a heeft, enzovoorts.
element[a].next is dan b, dat moet worden e.
element[b].previous was a, dat moet worden e.
Dan moet van element[e] de waarde voor next en previous worden gezet op b en a.
element[e].parent wordt gelijk gemaakt aan element[a].parent.

Insert before

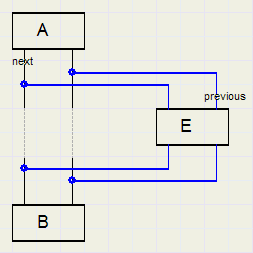
Deze bewerking zal worden gebruikt om een element in te voegen voor het eerste child element.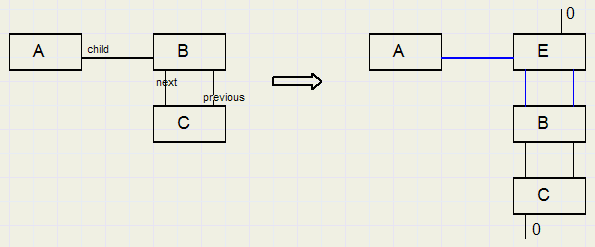
In de figuur hierboven zijn B en C children van A.
Element E wordt ingevoegd voor B.
De waard next van element e en previous van element B moet worden aangepast.
Element[a].child wordt e inplaats van b.
Element[e].parent = a.
Merk op dat element[e].previous = 0.

Insert child

Deze bewerking voegt het eerste kind toe aan een parent.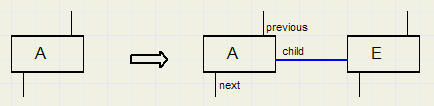
next en previous van element E zijn 0.

delete

Delete verbergt een element. Daarbij blijft de informatie van dat element behouden.
Alleen de koppeling met de boom wordt verbroken.
Daardoor kan later (met een Undo opdracht) de wijziging weer ongedaan worden gemaakt.
In het plaatje hieronder wordt element E verwijderd met kinderen C,D,F en al.

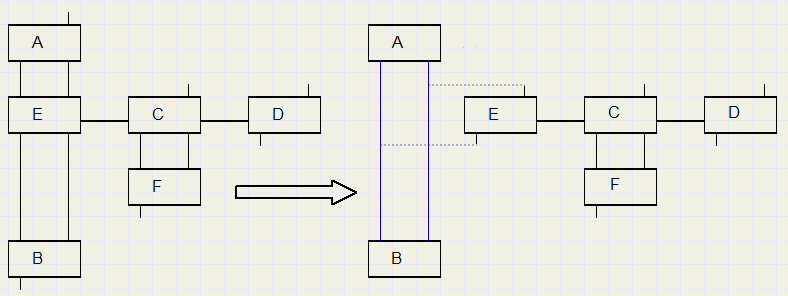
Replace

Deze bewerking vervangt een element door een ander.
De informatie van het vervangen element blijft behouden, zodat de wijziging later ongedaan
kan worden gemaakt.
Replace kan worden gebruikt als de eigenschappen van een element zijn gewijzigd.
In het plaatje hierna is C een ongebruikt element, dat E vervangt.

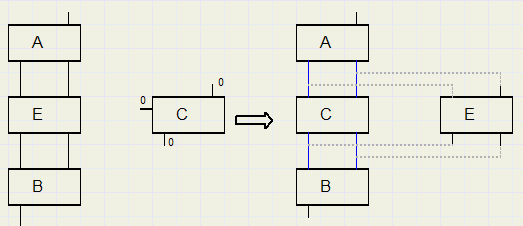
Pack

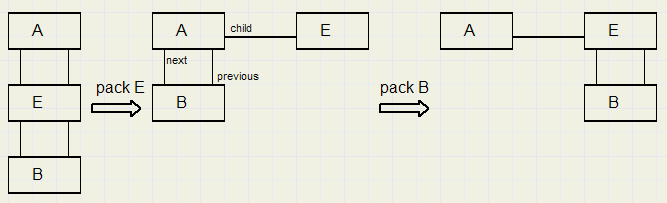
Deze bewerking maakt van een -next- element een child van het voorgaande element.
Dat vorige element zal gewoonlijk net zijn ingevoegd om parent te worden van een rijtje volgende elementen.
In het plaatje hierna staat een boom met daarna het resultaat van een pack E gevolgd door een pack B opdracht.

Undo

De undo opdracht maakt één van de voorgaande bewerkingen ongedaan.
Het -undo- systeem kan bijvoorbeeld zijn ingericht voor het onthouden van een beperkt aantal opdrachten.
Dat is het aantal opdrachten dat ongedaan gemaakt kan worden.
In een array[1..] undolist staat dan een code voor de bewerking en het nummer van het element.
In het lijstje hieronder staat bij elke bewerking de tegengestelde bewerking
    insert afterdestroy
    insert beforedestroy
    insert childdestroy
    deleterestore
    replacereset
    packunpack

destroy

De destroy opdracht verwijdert een element uit de boom en zet alle velden op 0.
Het elementtype wordt op free gezet, zodat het element voor een volgende opdracht gebruikt kan worden.

restore, reset, unpack

Deze bewerkingen hebben geen nadere toelichting meer nodig.
Toch nog één: bij reset wordt het vervangende element op 0 gezet zoals bij een destroy opdracht.

Het undo bereik

Stel, dat we de laatste 10 opdrachten bewaren, zodat we altijd 10 stappen terug kunnen gaan.
Bij de elfde stap moeten dan alle opdrachten in het undo-array één plaats opschuiven, waarbij stap 1 wordt overschreven
en stap 10 vrijkomt om de volgende opdracht op te slaan. Was stap 1 een insert (achter, voor of kind) of een pack opdracht, dan is geen aktie nodig.
Was het echter een delete of replace opdracht dan moet het betreffende, niet actieve, element worden vrijgegeven,
er wordt dan een destroy opdracht op dit element uitgevoerd.

De Tree exerciser

Het programmeren van bewerkingen op de bomen met elementen leidt gemakkelijk tot fouten.
Daarom is het zaak e.e.a. grondig te testen voordat de structuur wordt toegepast.
Temeer omdat in geval van een meerdere pagina's tellende editor het om duizenden elementen gaat.
Hieronder staat een verkleinde afbeelding van de exerciser
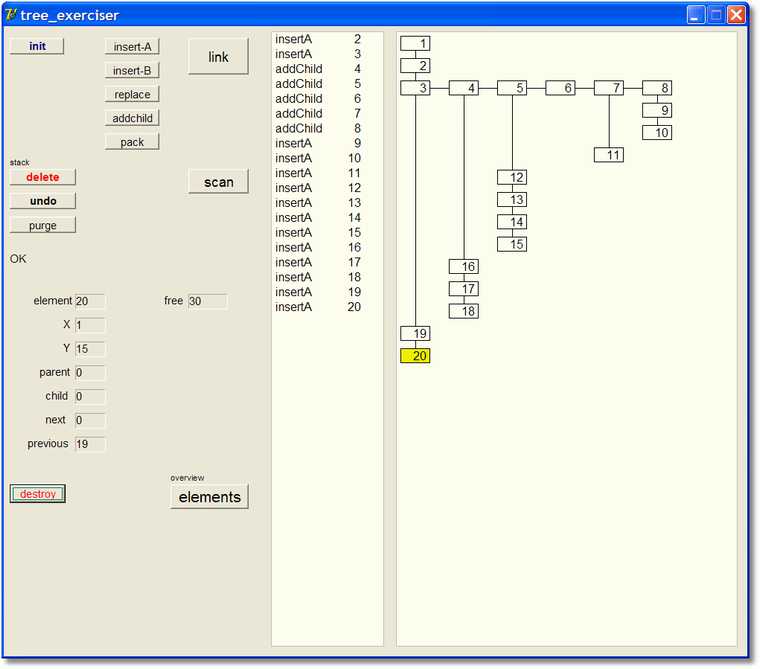
Element 1 staat linksboven en kan niet worden verwijderd.
Children staan rechts van hun parent getekend.
Elementen die onder elkaar zijn getekend en zijn verbonden hebben dezelfde parent.
Er is één verbindingslijntje getekend, dat staat dus voor zowel next als previous
of voor parent en child van de verbonden elementen.
Er is altijd één element gemarkeerd (met de kleur geel).
Een ander element is te markeren door er met de muis op te klikken.
Bewerkingen hebben betrekking op het gemarkeerde element.
Buiten de reeds besproken bewerkingen zien we de knoppen

init

Om alle elementen op 0 te zetten en alle opdrachten uit het undo-array te verwijderen.
(er is plaats voor 50 elementen en 25 undo stappen)

purge

Schuift de undo stack één plaats omhoog. Zie hiervoor "het undo bereik".

destroy

Zet het gemarkeerde element op 0.
Deze opdracht zal in de regel niet rechtstreeks worden uitgevoerd, maar het gevolg zijn van
een undo opdracht of een undo-stack-purge.

scan

Een druk op deze knop roept de scanElement( ) functie aan, die het volgende of vorige element
in de boom levert op grond van de vorige stap.
Met scanElement kan de gehele boom van voor naar achter en weer terug worden doorlopen.
Deze functie wordt gebruikt om de boom te tekenen en ook bij de destroy opdracht om hele takken
vrij te geven.
type TTreemove    = (tmNone,tmParent,tmChild,tmNext,tmPrevious);

function ScanElement(var elmnt : dword; tm : TTreeMove) : TTreeMove;
tm is de voorgaande treemove.
Gebruik tm = tmChild om in voorwaartse richting te scannen.

Link

Elke opdracht in de undolist heeft een veld met de boolean variabele link.
Door linking kunnen twee undo opdrachten worden verbonden.
Bij een undo opdracht zullen alle voorgaande opdrachten ongedaan worden gemaakt die met een link zijn verbonden.
Stel dat opdrachten 10,11,12 gelinkt zijn (deze elementen zijn bijvoorbeeld samen ingevoegd).
Opdrachten 11 en 12 hebben dan de link flag = true staan. Bij undo wordt eerst 12, dan 11, dan 10 ongedaan gemaakt.
10 heeft geen link flag aanstaan, zodat dit de undo opdracht daarna stopt.

Overview elements

Indrukken geeft de status aan van alle 50 elementen.
Actieve elementen zijn zwart getekend, ge-delete elementen zijn rood en ongebruikte elementen zijn groen.

Hieronder geef ik nog alle velden van een element, zoals deze voor dit project zijn gedfinieerd
const maxelement = 50;
      maxaction  = 25;  //undo actions
	  
type TElmntAction = (eaNone,eaInsertA,eaInsertB,eaDelete,eaReplace,
                     eaAddChild,eaPack);
     TElementStatus = (esFree,esDeleted,esActive);
     TElementtype = (elFree,elActive);
     TElement = record
                 eltype : TElementType;
                 marked : boolean;
                 x,y    : word;
                 parent : dword;
                 child  : dword;
                 next   : dword;
                 previous : dword
                end;
      TEditAction = record
                     elmnt  : dword;
                     action : TelmntAction;
                     bwlink : boolean;   //backward link
                    end;

var element : array[1..maxelement] of TElement;
    undolist : array[1..maxaction] of TEditAction;
    lastAction : word;
    freeElementcount : dword = 0;
Voor verdere details verwijs ik naar de source listing of de complete source code van dit project.
(zie top van deze pagina)