binaire puzzel oplossingen tellen

Binaire puzzel oplossingen

download program

download Delphi project

(Met dank aan de heer Jelle van der Linde, die de vragen stelde en informatie leverde)

Hieronder staat een binaire puzzel zoals in kranten wordt aangetroffen.
Links de originele, rechts de opgeloste.

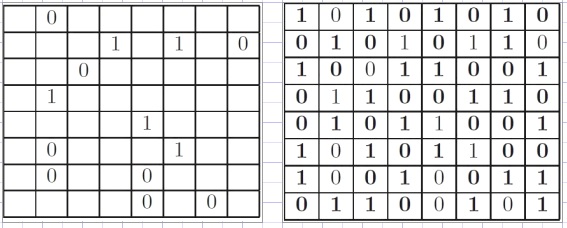
In de lege cellen moet een "1" of een "0" worden ingevuld maar:

Binairy puzzels komen in de formaten 4x4, 6x6, 8x8 (zoals hierboven),10x10, 12x12 of 14x14.
Een goede puzzel heeft één unieke oplossing.
De vragen rijzen:

De laatste vraag is ook te schrijven als:

Dit Delphi project gaat in op de laatste vraag.
Maar vandaar is het antwoord op de andere vragen een kleine stap.
In het algemeen zijn dit soort problemen analytisch of numeriek aan te pakken.

De numerieke aanpak is gekozen.
Neem als voorbeeld een 6x6 puzzel. Met 6 bits maken we getallen 0 tot 63.
Door de beperkende regels blijven er 14 getallen over, zie hieronder:

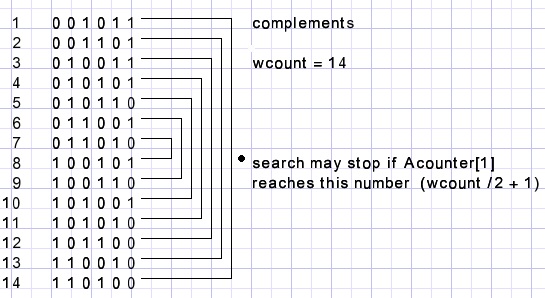
Om overbodig werk te vermijden worden deze getallen eenmaal aangemaakt en in een tabel (numbers[ ]) bewaard.
In plaats van deze getallen gebruiken we de index van de numbers tabel om een rij of kolom aan te duiden.
Als rijen worden ingevuld met geldige getallen uit de numbers[ ] tabel,
kunnen kolommen ontstaan met ongeldige getallen.
Het is handig om per getal te weten of het geldig is.
Array VNlist[number] of Boolean bevat true voor een geldig getal.
VNlist[ ] heeft voor een n x n puzzel 2^n elementen (true of false).
Om alle puzzel oplossingen systematisch weer te geven is een telwerk nodig.
Dat is array Acounter[1..bitcount ] waarvan elk element verwijst naar het numbers[ ] array.
Een element van Acounter is als cijfer te beschouwen van het getal Acounter[ ].

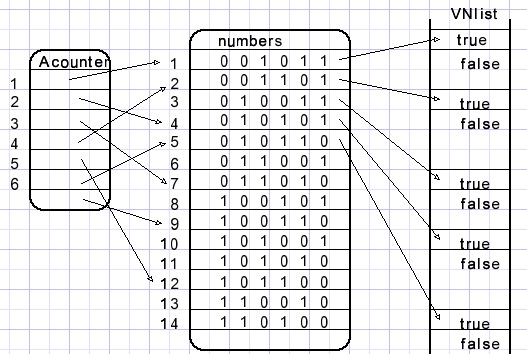
Bij een n x n puzzel heeft Acounter[ ] n elementen.
De VNlist heeft 2^n elementen.
Alle rij getallen zijn geldig omdat ze uit het numbers[ ] array komen.

Geldige getallen voor een n x n puzzel

Bij het schrijven van een volgende rij kunnen we al vermijden dat er twee nullen of enen in de kolom komen.
Voor dit doel definiëren we

 
Var bitcountmask : word;//2^n - 1; 111111 voor een 6x6 puzzel, 11111111 voor 8x8
        Amask : array[1..14] of word;
        AFixed : array[1..14] of word;

Voor rij n {n > 2}

procedure makeFixedbits(n : byte);
var N1,N2,X : word;
begin
 N1 := numbers[Acounter[n-1]];
 N2 := numbers[Acounter[n-2]];
 X := N1 xor N2;
 Amask[n] := x xor bitcountmask;
 AFixed[n] := N1 xor bitcountmask;
end;

Voorbeeld (6x6 puzzel)

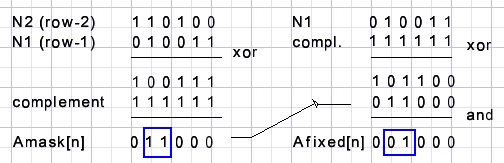
In rij n moeten bits 3 en 4 "1" en "0" zijn om te vermijden dat er 3 dezelfde bits onder elkaar staan.
Als alle 6 rijen zijn ingevuld zijn deze controles nodig:

1.
Elke nieuwe rij (Acounter[ ] element) wordt met de vorige vergeleken.
2.
Voor de kolom tests worden de kolommen als rijen geschreven door
de cellen te spiegelen over de diagonaal van rechtsboven naar linksonder.
Dat is een tijdrovend proces dat te verkorten is door de rijen met getallen op te tellen.
Een 6 x 6 puzzel heeft namelijk per kolom drie enen zodat de gesommeerde rijen de waarde
3*111111(bin)=189 moeten hebben.
Algemeen: bij n * n puzzels is deze waarde (n/2)(2^n - 1).
Dat elimineert al veel foute getallen en alleen als deze test goed is schrijven we de kolommen als rijen
in array VGame[ ].
3.
Een geldig getal wordt aangegeven in array VNlist[getal].
4.
Om gelijke kolommen op te sporen moeten alle getallen in VGame[ ] met elkaar worden vergeleken.

De sommering van rijen bespaart 65% van de tijd bij een 8x8 puzzel.
Oplossingen van een binaire puzzel bestaat uit complementen.
Bij verwisseling van "0" en "1" onstaat immers weer een oplossing.
De helft van de tijd is dus te besparen door niet de complementen te tellen.
Het tellen stopt als Acounter[1] het eerste complementaire getal in numbers[ ] aangeeft. (boven n/2).
Oplossingen tellen van een 8 x 8 puzzel is hiermee teruggebracht tot 4,3 seconden.
Bij een 10 x 10 puzzel telt het programma 4 miljoen oplossingen per minuut.
Verwachte tijd voor alle oplossingen is 16 uur.

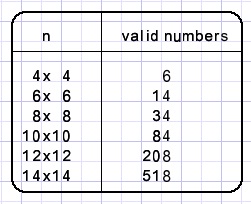
Resultaten

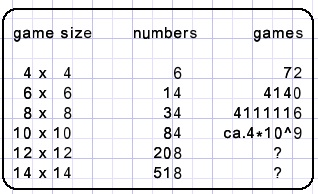
Het ziet er uit dat het aantal oplossingen van lege puzzels met een factor 1000 oploopt
voor elke volgende (even n x n) grootte.

Het programma

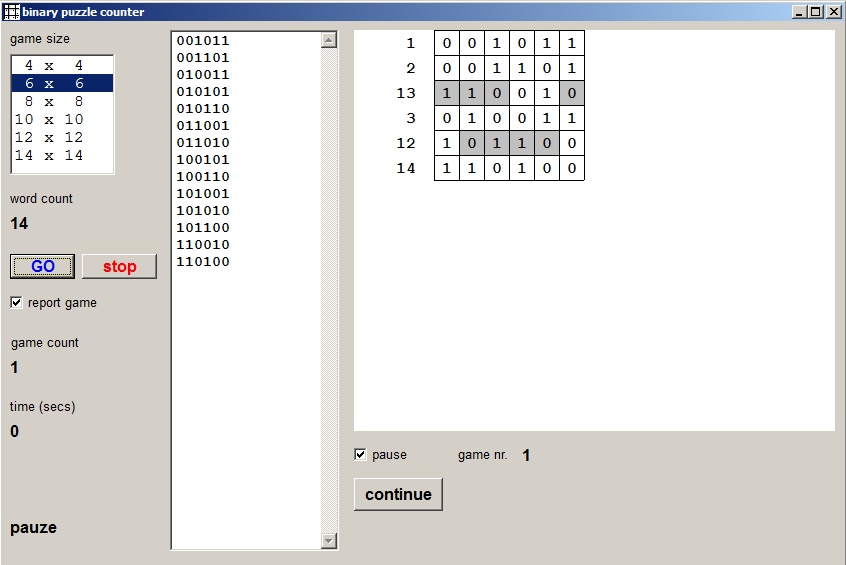
De kern van het programma is:

 
function NextAcount : boolean;

Die verhoogt Acounter en levert true voor een nieuwe puzzel.
Wcount (word count) is het aantal geldige getallen in array numbers[].
LInc is een label.
Bitcount = 4 voor 4x4 puzzels, 8 voor 8x8….
NextAcount levert false als Acounter[1] verwijst naar een getal met MSB=1 (MSB is hoogste bit).
Dat voorkomt het tellen van complementaire puzzels.
Dit is de flowchart:

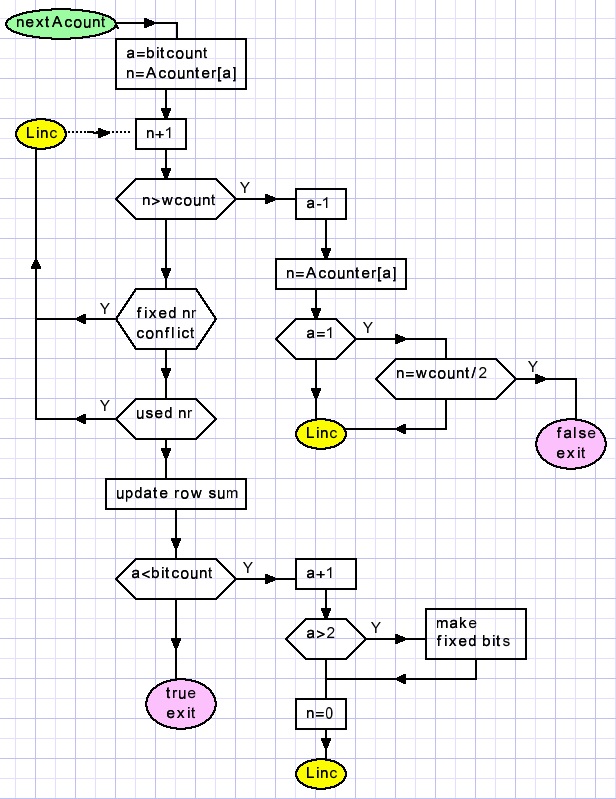
Opmerking: het gebruik van een label en GOTO statements leidt hier tot beter leesbare code
dan gestructureerd programmeren met while en repeat statements.

Andere fucties en procedures zijn:

function testValid(w : word) : boolean;

Levert true als een getal "goed" is, zie de restricties.

procedure MakeNumbers;

Maakt de numbers[ ] en VNlist[ ] arrays.

procedure makeFixedbits(ai : byte);

Berekent de AMask[ai ] en AFixed[ai ] waarden om foute kolommen te vermijden.

function UsedWord(a : byte; wix : word) : boolean;

Levert true als index wix niet voorkomt in Acounter[1..a-1]. Voorkomt gelijke rijen.

procedure setGame1;

aangeroepen bij de start om het eerste puzzel te maken.

procedure makeVGame;

Zet de kolommen om naar rijen in array VGame[ ].

function checkVGame : boolean;

Levert true als VGame[ ] goede getallen bevat.

Hier eindigt de beschrijving van de binaire puzzel oplossingen teller.
Voor details verwijs ik naar de source code.

Dit programma zal later worden aangepast om een helper/oplosser van binaire puzzels te worden.