De beste stoel in een stadion

Dit meetkunde probleem is afkomstig van Omid Motahed, docent wiskunde in Beijing.

Dit is de vraag:
Wat is de beste zitplaats in een voetbalstadion?

Kijk eens naar het volgende plaatje:

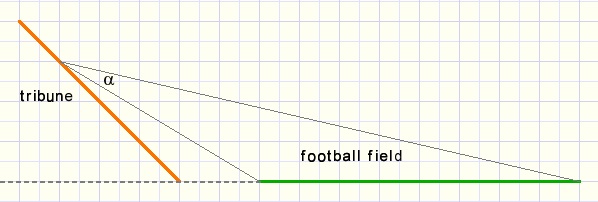
Een toeschouwer ziet het speelveld onder een hoek a
Hoe groter die hoek, hoe beter.

Voor de oplossing van dit probleem gebruiken we de stellingen van Thales, zie hier:

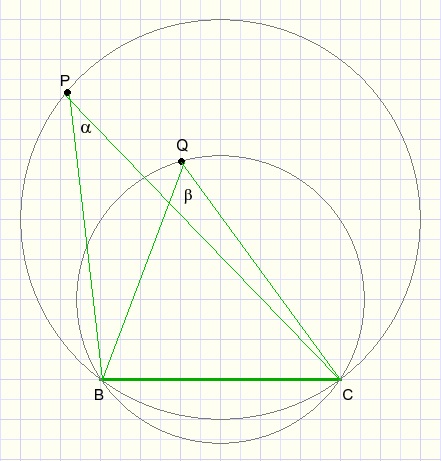
Voetbalveld BC is getekend als koorde van een cirkel.
Een stelling van Thales zegt:
vanaf elk punt op de omtrek van een cirkel zien we een koorde onder dezelfde hoek.
Deze hoek is de helft van de hoek gezien vanuit het middelpunt.
Dus LBPC is gelijk voor elk punt P op de cirkel.
Ook is LBQC gelijk voor elk punt Q op de kleinste cirkel.
Hoe kleiner de straal van de cirkel hoe groter de hoek.
(want de koorde is dan relatief groter)
Zie het volgende plaatje:

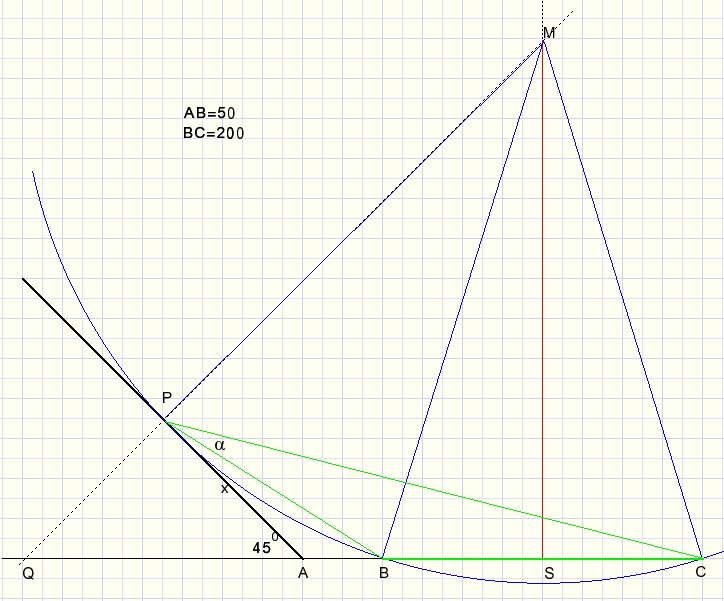
Het probleem kunnen we nu anders stellen als:

zoek de kleinste cirkel die door de punten B,C,P gaat Die cirkel heeft AP als raaklijn.

Gegeven zijn:

Berekening van x = AP:

Berekening van a

⁰