Analytische meetkunde (staatsexamen 1934)
Onderstaande opgaven komen uit het staatsexamen analytische meetkunde van 1934.
De uitwerking en antwoorden zijn van mijzelf.

Opgave 1

Van een driehoek ABC is de basis AB vast, de top is veranderlijk.
Gegeven is nog dat geldt: tan A . tan B = 3.
Bepaal de meetkundige plaats van C.

Uitwerking:
Met meetkundige plaats wordt bedoeld: welke functie of grafiek maken alle punten C samen?

eerst eens een plaatje tekenen:
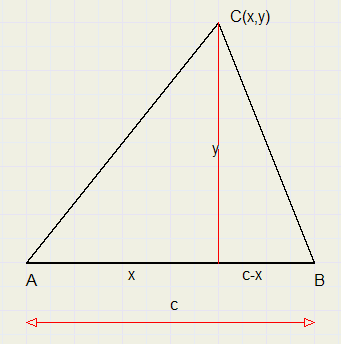
De lengte van basis AB noemen we c (zijde tegenover hoekpunt C)

Zodat gelden moet:
y
x
 · 
y
c − x
 = 3

oftewel: y2 = 3x(c - x)

We kunnen met dit antwoord genoegen nemen.
Anno 2014 zouden we deze vergelijking plotten om te zien hoe de oplossing er uit ziet.
Maar in 1934 beschikte men nog niet over slimme machientjes.
Reden om de vergelijking eens nader te bekijken.

Zowel y als x komen in het kwadraat voor (werk de haakjes maar weg).
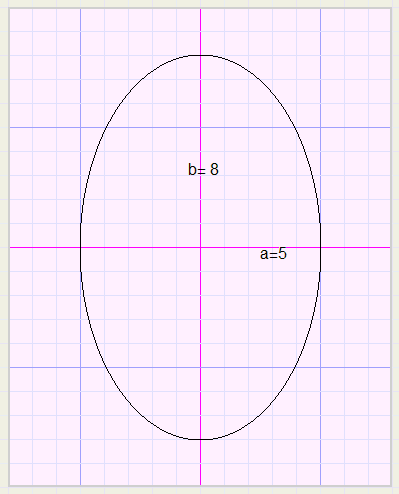
Dat duidt op een ellips.
Bovendien zien we dat y = 0 voor x = 0 en ook voor x = c.
De ellips zal dus een halve horizontale middellijn hebben van lengte c/2.
De vertikale as gaat dan door (c/2 , 0).
De top is dus 3c/2 (c / 2) = 3 
2
æ
c
2
ö
­­
èø
 = 
2
æ
\3
 · 
c
2
ö
­­
èø

Bovenstaande waarde is ook de halve lengte van de vertikale middellijn.

De algemene vergelijking van een ellips met middelpunt (0,0) is
    2
    æ
    x
    a
    		ö
    ­­
    èø
     + 
    2
    æ
    y
    b
    		ö
    ­­
    èø
     = 1
In ons geval vindt een horizontale verschuiving plaats van c/2 naar rechts,
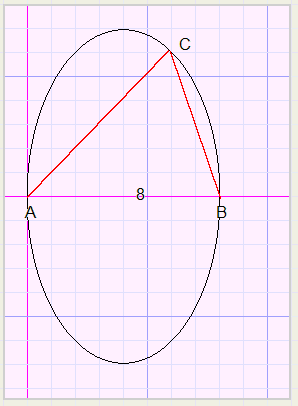
zodat x moet worden vervangen door (x - c/2).
De vergelijking wordt:
     
    2
    æ
    y
    c
    2
     
    \3
    		ö
    ­­
    èø
    		 
     + 
     
    2
    æ
    x − 
    c
    2
    c
    2
    		ö
    ­­
    èø
    		 
     = 
         		 
    1
     
Uitwerking:
    y 2 + 3 
    2
    æx − 
    c
    2
    		ö
    ­­
    èø
     = 3 
    2
    æ
    c
    2
    		ö
    ­­
    èø

    y 2 = 3 x (c − x)
Dit antwoord was ook verkregen door in y2 = 3x(c - x) het kwadraat (x - c/2) af te splitsen:
    y 2 + 3 (x 2 + c x) = 0
    y 2 + 3 
    2
    æx − 
    c
    2
    		ö
    ­­
    èø
     = 
    3 c 2
    4
    enzovoorts
tenslotte de grafiek van alle punten C
gekozen is AB = 8, zodat de halve vertikale middellijn een lengte heeft van de wortel uit 48

Opgave 2

Langs de parabool y2 = 2px bewegen zich twee punten P en Q zo,
dat steeds yQ = -2yP blijft.
De raaklijnen in P en Q snijden elkaar in S.
Men vraagt de meetkundige plaats van S.

Uitwerking:
We zien hier een parabool waarvan de x-as de symmetrieas is. De top ligt in de oorsprong van het assenstelsel.
De punten P en Q liggen aan weerskanten van de x-as.

We schrijven op wat we "weten" :
    yP 2 = 2 p xP
    yQ 2 = 2 p xQ
    yQ = −2 yP
Een beetje combineren levert op
    xQ = 4xP
Wellicht kenden de examinanten de formule voor de raaklijn uit het hoofd:
    parabool y2 = 2px..........{top in (0,0) afstand brandpunt tot richtlijn = p}
    raaklijn in punt (x1,y1):
    y = 
    p
    y1
     (x + x1)
Aan het einde van deze opgave zal ik de formule afleiden.

De raaklijnen:
    in P: y = 
    p
    yP
     (x + xP)
    in Q: y = 
    p
    yQ
     (x + xQ)
    zodat:
    in Q: y = 
    p
    −2 yP
     (x + 4 xP)
zodat (coördinaten van snijpunt S):
    x + xP = −
    1
    2
     (x + 4 xP)
    x = -2xP........ y = 
    −yP
    2
Schrijven we voor xP =
yP 2
2 p
dan krijgt S de coördinaten:
    (
    −yP 2
    p
     ,
    −yP
    2
     )
yP is hierin de enige variabele, we stellen y = -yP/2 dus yP = -2y en de coördinaten van S gaan over in
    (
    −4 y 2
    p
     , y)
Hier staat dus de vergelijking
    x =
    −4 y 2
    p
    of
    y 2 = −
    p
    4
     x
dat is een parabool met symmetrieas de x-as, opening naar links en top op (0,0).

Hieronder een grafiek met de waarde p = 4


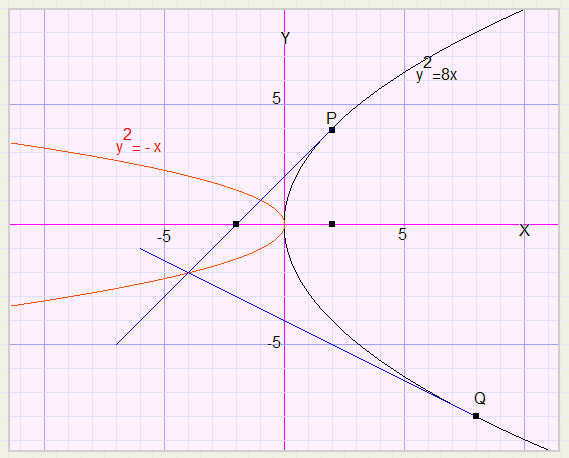
Toelichting bij opgave 2

1. Liggende parabool (x-as is symmetrieas)
Een parabool is de meetkundige plaats van de punten die gelijke afstand hebben tot een punt
(brandpunt) en een lijn (richtlijn).
We nemen als richtlijn x = -p en als brandpunt (p,0)
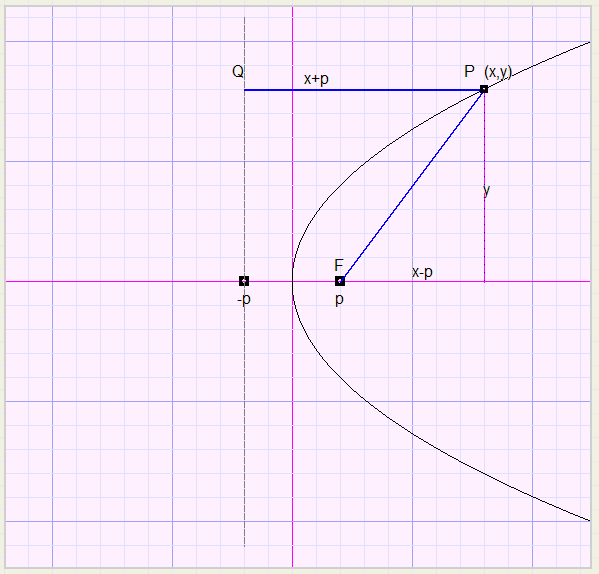
Punt P is een willekeurig punt op de parabool.
Uit PF = PQ volgt:
    (x + p)2 = (x - p)2 + y2
    x2 + 2xp + p2 = x2 - 2px + p2 + y2
    y2 = 4px
Dat is dus een parabool met brandpuntsafstand p.

2.De raaklijn in een punt (a,b) van parabool y2 = 2px
(brandpuntsafstand dus p/2 of: p is de afstand tussen brandpunt en richtlijn)

Ik kies hier voor een meetkundiger aanpak en ga uit van het gegeven dat horizontale stralen
weerkaatst worden door het brandpunt.
(zie hiervoor mijn artikel over parabolische spiegels)
Een punt P op de parabool heeft coördinaten (a,b)
Eenvoudig is in te zien, dat hoeken met gelijke tekentjes even groot zijn.
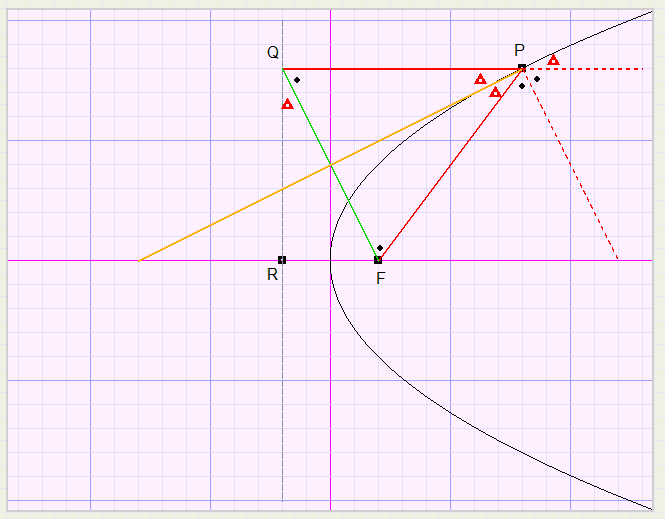
Wegens gelijkvormigheid is de richtingscoëfficient van de raaklijn RF / RQ = p / b
Zodat de raaklijn de vergelijkking heeft
    y − b = 
    p
    b
     (x − a)
    dus
    y = 
    p
    b
     (x − a) + b
    y = 
    p
    b
     x − 
    a p
    b
     + 
    b 2
    b
    y = 
    p
    b
     x − 
    a p
    b
     + 
    2 a p
    b
    en resultaat:
    y = 
    p
    b
     (x + a)