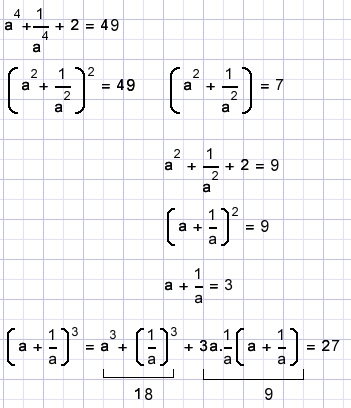| Algebra problemen (70A..D) |  |
Probleem A
Gegeven is:x,y,z zijn positieve gehele getallen.
3x = 4y = 5z
Bereken de kleinst mogelijke waarde van x + y + z.
Oplossing A
Stel 3x = 4y = = 5z = K, zodat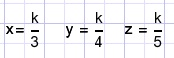
dan is:
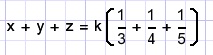
en omdat KGV(3,4,5) = 60
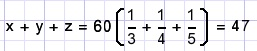
Probleem B
x + y = y + z = x + z = xyz.Bereken x,y,z.
Oplossing B
x = y = zzodat:
-
2x = x3
x(x2-2)=0
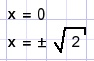
Probleem C
x + y + z = 0x2 + y2 + z2 = 14
x3 + y3 + z3 = 18
Vraag:
xyz = ?
x,y,z = ?
Oplossing C
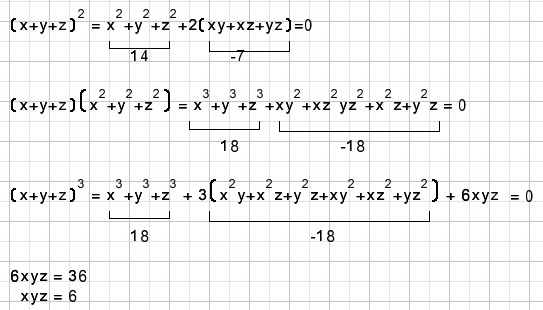
Om x,y,z afzonderlijk te berekenen is het handig om ze te beschouwen als oplossingen van
-
(t-x)(t-y)(t-z) = 0
zodat
t3 - t2(x+y+z) + t(xy + xz + xz) - xyz = 0.
Omdat (eerder berekend) x+y+z =0 en xy+xz+yz=-7 en xyz=6 .....
t3 - 7t - 6 = 0
(t+1)(t-2)(t-3) = 0
x = -1
y = -2
z = 3
Probleem D

Oplossing D