

| Alegra problemen 66A, 66B |  |
Probleem 66A
Bewijs dat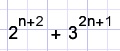
deelbaar is door 7 voor elke waarde van n {n is positief geheel getal}
Probleem 66B
Bewijs dat de breuk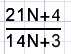
voor geen enkele waarde van N is te vereenvoudigen.
Probleem 66C
x en y zijn positieve gehele getallen.Bewijs dat wanneer 2x+3y deelbaar is door 17 dan ook 9x+5y deelbaar is door 17.
Oplossing 66A
Dit is een bewijs met "volledige inductie".Stel dat de bewering klopt voor een bepaalde waarde van n.
We onderzoeken of daaruit volgt dat de bewering ook klopt als n wordt vervangen door (n+1):

De bewering klopt voor n=1.
Dus ook voor n=2,3,4,......
Oplossing 66B
Opmerking: met GGD(A,B) bedoelen we de grootste gemeenschappelijke deler van A en B.We gebruiken de stelling van Euclides die stelt dat GGD(A,B) = GGD(A-B,B).
GGD(21N+4,14N+3)=GGD(7N+1,14N+3)=GGD(14N+3,7N+1)=
GGD(7N+2,7N+1)=GGD(1,7N+1)=1
Er zijn geen gemeenschappelijke factoren, de breuk is niet te vereenvoudigen.
Oplossing 66C


