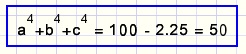| Algebra probleem (5) |  |
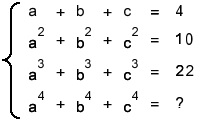
Dit probleem is op twee manieren aan te pakken:
-
1. door a,b en c op te lossen en die waarden in regel 4 te substitueren.
2. door regel 4 uit te drukken in de waarden van regels 1 t/m 3
Een wat intu´tieve aanpak.
We zien gehele getallen.
Dat maakt dat a,b,c geen breuk kunnen zijn.
Maar a,b en c kunnen ook geen gehele getallen zijn.
Uit de kwadratensom volgt nog dat de absolute grootte van a,b en c drie of minder is.
De kwadraten van wortels van gehele getallen zijn ook gehele getallen.
In regels 1 en 3 moeten dan wortels tegen elkaar wegvallen.
| Wat dus overblijft is een vorm |  |
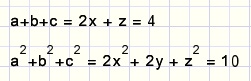
Nu kunnen we de vergelijkingen schrijven
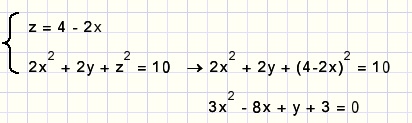
In deze laatste regel beschouwen we y+3 even als constante.
De ABC formule voor x levert
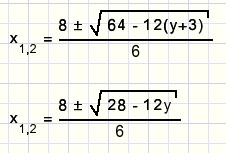
Voor y = 1 wordt x = 2 en a = 1, b = 0, c = 3.
Dat klopt niet voor de vergelijking met de derde machten.
Neem y = 2.
Dan wordt x = 1 en z = 2. (geheel getal)
| Dat levert | 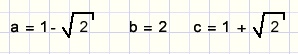 |
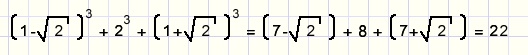
Dat klopt, de opossing is juist.
Ingevuld in de vierde regel:
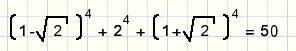
2.
Oplossing zonder a,b,c afzonderlijk te berekenen.
We trachten a4 + b4 + c4 uit te drukken in de eerste drie regels.
Meer eerst even een zijsprong om werk te besparen.
Dit probleem is symmetrisch.
a,b en c kunnen van plaats wisselen zonder dat het antwoord verandert.
Bij het uitschrijven in termen van bijvoorbeeld (a+b+c)4 bestaan de termen uit 4 letters
in alle mogelijke volgorden.
Bijvoorbeeld aaaa, aabc, cbba ....
We gaan bij de combinatoriek te rade hoe vaak een term dan voorkomt:
Vier verschillende factoren (zoals abcd) kunnen op 4! = 24 manieren op een rijtje staan.
Zijn echter 3 factoren gelijk (zoals in ab3) dan dient de 24 door 6 te worden gedeeld,
omdat 3 factoren op 3! = 6 manieren op een rijtje kunnen staan maar dat geen verschil maakt.
Zo zal de term a2b2.... 24/(2!2!) = 6 maal voorkomen.
De term abc2 komt 24/(1!1!2!) = 12 maal voor.
Daar gaan we:

Nu de volgende:

merk op: we schreven 6abc = 9abc - 3abc
Verder:
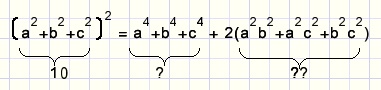
Hier verschijnt het antwoord bij ? maar wat te beginnen met ??

Het voorgaande combineren: