

| Algebra probleem (45) |  |
Probleem
Dit probleem is door Lahcene Belhadj geplaatst in de Facebook groep "Classical Mathematics".De oplossing is van mijzelf.
bereken
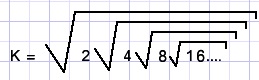
Oplossing
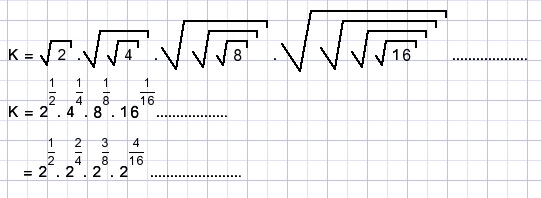
stel nu:
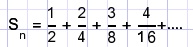
Bereken Sn voor n = 1, 2 3, 4, .....
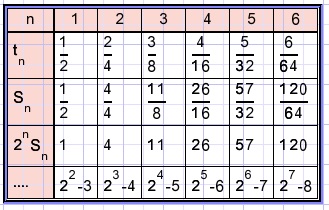
en we zien
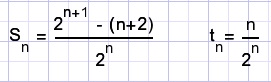
deze formule klopt voor n=1 tot n=6 maar daarna?
Om de algemene geldigheid vast te stellen moeten we aantonen dat Sn+1 = Sn + tn+1.
Immers, als Sn dan geldt voor n=1 dan ook voor n=2,3,....

Inderdaad.
Wat gebeurt met Snals n zeer groot wordt?
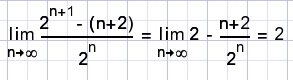
zodat K = 22 = 4.

