

| Algebra probleem (26) |  |
Deze puzzel werd aangetroffen op LinkedIn groep "Math Education" en was
ingediend door DEB JYOTI MITRA.
Van een rechthoekige driehoek is de omtrek 30 (meter) en de oppervlakte 30 (m2).
Bereken de lengte van de zijden van die driehoek.
Een beetje gokken geeft meteen het antwoord omdat de zijden een Pythagoras drietal moeten zijn:
(5, 12, 13) want
5 + 12 + 13 = 30 maar ook
5.12/2 = 30
Stel de rechthoekszijden a en b, de schuine zijde c.
Opgelost moet worden het stelsel:
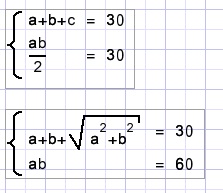
Vervelend hierin is de wortel.
De kunst is om daar snel vanaf te komen.
Oplossing 1
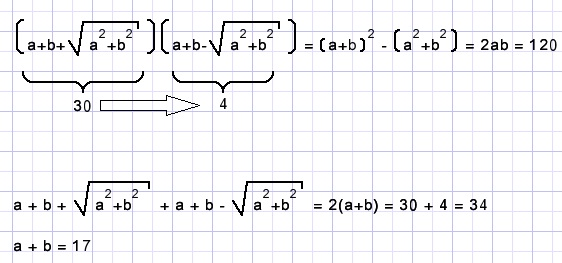
De vergelijking ab = 60 gaat nu over in
a(17-a) = 60
a2 - 17a + 60 = 0.
ABC formule:
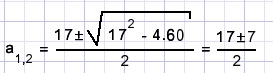
a1 = 5
a2 = 12
De zijden hebben lengte 5, 12 en 13.
Oplossing 2
(a+b)2 = a2 + 2ab + b22ab = 120
c = 30 - (a+b)
(a+b)2 = 120 + (30 - (a+b))2
(a+b)2 = 120 + 900 -60(a+b) + (a+b)2
60(a+b) = 1020
a+b = 17
ab= 60 wordt nu
a2 - 17a + 60 = 0.
Ontbinden in factoren:
(a-5)(a-12) = 0
De rechthoekszijden zijn 5 en 12 lang, de schuine zijde is 13.

