

| Algebra probleem (25) |  |
Als
a + b + c = 1 en
a3 + b3 + c3 = 4
bereken dan
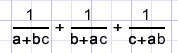
Oplossing
We berekenen eerst (a+b+c)3
Probleem zijn nu de noemers a+bc, b+ac, c + ab.
Optellen levert oeverloos gereken op.
Hoe dat te vermijden?
Bedenk dat (1-a)(1-b) = 1-a-b+ab
maar omdat 1-a-b=c geldt
(1-a)(1-b) = c + ab
Op eendere wijze is te schrijven:
(1-a)(1-c) = b + ac en
(1-b)(1-c) = a + bc
zodat
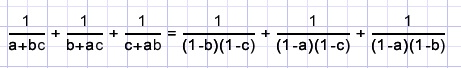
Gelijknamig maken van de breuken is nu simpel, optellen levert
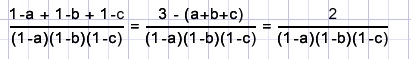
De teller is hiermee bekend, nu de noemer nog.
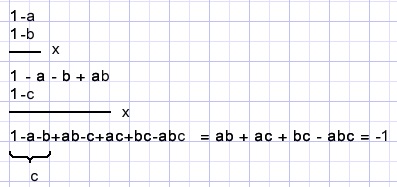
Het antwoord is 2/(-1) = -2.

