Algebra probleem (17)

Gegeven is de curve met de vergelijking:
    x3 + y3 - x2 - y2 + 3xy = 0
Gevraagd:
    de afgeleide (richtingscoëfficient) in het punt (0,0).
Dit is een zogenaamde impliciete functie, d.w.z. van het type f(x,y) = 0.
De grafiek ziet er zo uit:



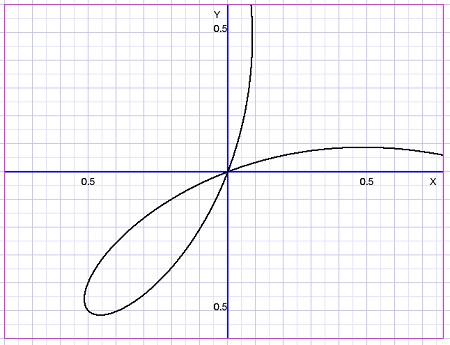
Differentiëren levert op:
    3x2+3y2y'-2x-2yy'+3y+3xy'=0
Voor (0,0) ontstaat 0 = 0. Dat schiet niet op.

We trekken een rechte lijn y = ax door de oorsprong en berekenen de snijpunten met de curve.
Voor y vullen we ax in:
    x3 + (ax)3 - x2 - (ax)2 + 3ax2 = 0.
    x2[x(1 + a3 ) - 1 - a2+3a] = 0
Of x2 = 0, x = 0
Of x(1 + a3 ) - 1 - a2+3a] = 0.



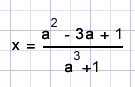
De lijn mag de curve maar in één punt snijden( =raken) zodat moet gelden: x = 0.
    a2 - 3a + 1 = 0.
ABC formule:



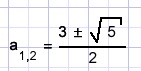
is het antwoord.

Parameter functies
Vanaf hier is het maar een kleine stap om de curve te schrijven als parameter functie.
Die heeft de algemene vorm:
    y = f(t)
    x = g(t)
zowel x als y zijn hier functies van een derde variable die meestal t wordt genoemd.
Hierboven echter zien we geen t maar a, de helling van de curve.
We kunnen nu x en y als functie van a schrijven, bedenkend dat y = ax



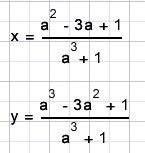
Laat bijvoorbeeld a met kleine stapjes lopen van -50 naar 50 en bereken steeds (x,y).
Het tekenen van de curve gaat nu vele malen sneller dan bij een impliciete functie waarbij elk punt (x,y)
onderzocht moet worden op ligging op de curve.