Algebra probleem (12)

In de Omid Motahed "Classical Mathematics" Facebook groep worden wiskundige problemen
en oplossingen gepost.
Onderwerpen zijn analyse, getaltheorie, meetkunde en computer software.

Opmerking: Omid Motahed is wiskunde leraar in Beijing.

Recent trof ik wederom een prachtig probleem aan met drie verbazingwekkende oplossingen.
Lees dus vooral verder.
Dit probleem is van Tilikraj Kaushal
als gegeven is:
    x2 + y2 + xy = 9
    x2 + z2 + xz = 16
    y2 + z2 + yz = 25
bereken dan
    xy + xz + yz = ?
oplossing 1 (Bikiran Das)
oplossing 2 (Paul Christian Abbott)
oplossing 3 (Dr. Kevin Wang)


Handgeschreven tekst heb ik naar mijn (DavDoc) wiskunde editor overgebracht.
Aan oplossing 3 heb ik een toelichting toegevoegd.

Oplossing 1.

(Bikiran Das)



Oplossing 2.

(Paul Christian Abbott)

Omdat de vergelijkingen homogeen zijn is een simpele benadering om te schrijven:
    y = ax
    z = bx
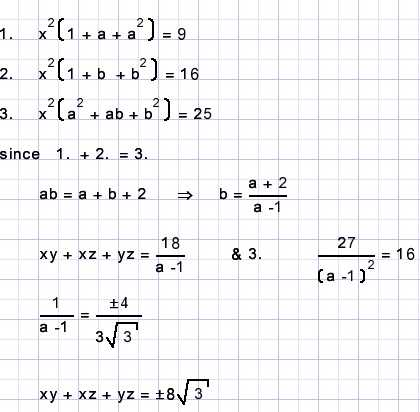
De drie vergelijkingen gaan dan over in:



Oplossing 3.

(Dr. Kevin Wang)

Laat in driehoek ABC P het Fermat punt zijn
(d.w.z. de hoek APB=BPC=CPA=120 graden)
Stel x=AP, y=BP, z=CP.
Dan zien we door toepassing van de cosinusregel dat:
    AB=3
    AC=4
    BC=5
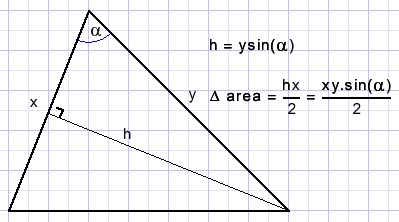
ABC is dus een rechthoekige driehoek met oppervlakte 6.
De oppervlakte kan ook geschreven worden als



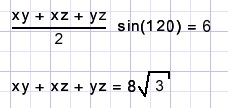
Toelichting bij deze oplossing:



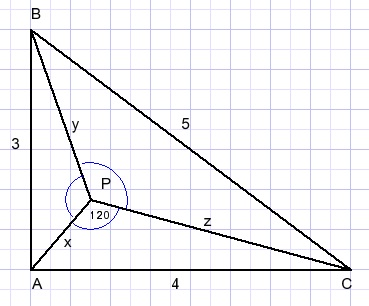
De cosinusregel toegepast op ΔAPB
    32 = x2 + y2 - 2xycos(120)
    since -2cos(120) = 1
    x2 + y2 + xy = 9
    etc.
De oppervlakte van een driehoek uitgedrukt in twee zijden met ingesloten hoek: