Algebra probleem (4)



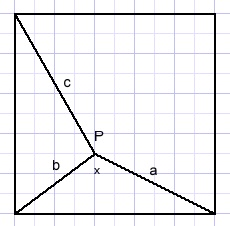
De figuur hierboven toont een vierkant met daarin een punt P zodanig, dat geldt:
    c2 = a2 + 2 b2
Vraag: bereken de grootte van hoek x.

Oplossing

Stel de zijde van het vierkant 1.
Stel de coördinaten van punt P(x,y).{andere x dan de hoek}
Neem als oorsprong de linker-onderhoek van het vierkant.



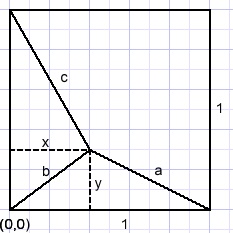
Pas de stelling van Pythagoras toe, dan is:
    a2 = (1-x)2 + y2
    b2 = x2 + y2
    c2 = x2 + (1-y)2
Dit invullen in het gegeven c2 = a2 + 2 b2 levert:
    x2 + (1-y)2 = (1-x)2 + y2 + 2(x2 + y2)
    haakjes wegwerken:
    1 - 2y + y2 + x2 = 1 - 2x + x2 + y2 + 2x2 + 2y2
    vereenvoudigen:
    x2 + y2 + y - x = 0.
Die vergelijking is een cirkel met verschoven middelpunt.
We kunnen ook schrijven:

of:

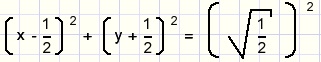Dit is een cirkel met straal 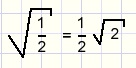en middelpunt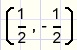



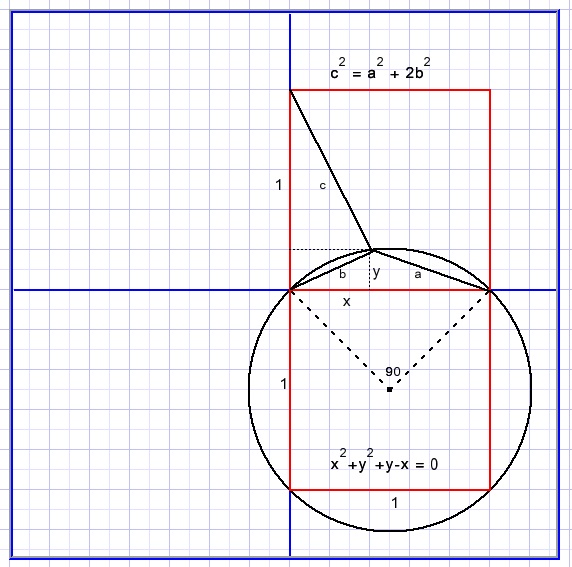
Zoals te zien staat de hoek x op een cirkelboog van 2700 zodat:
    x = 1350